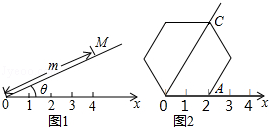
阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
| A.(60°,4) | B.(45°,4) |
C.(60°,2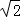 ) ) |
D.(50°,2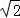 ) ) |
下列运算中错误的是()
A. + + = =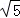 |
B. × × = = |
C.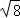 ÷ ÷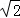 =2 =2 |
D.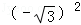 =3 =3 |
如果ab>0,a+b<0,那么下面各式:① =
= ,②
,② •
• =1,③
=1,③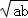 ÷
÷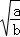 =﹣b,其中正确的是()
=﹣b,其中正确的是()
| A.①② | B.②③ | C.①③ | D.①②③ |
如图所示,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形还需要条件()
| A.AB=DC | B.∠1=∠2 | C.AB=AD | D.∠D=∠B |
如图,已知△ABC,以点B为圆心,AC长为半径画弧;以点C为圆心,AB长为半径画弧,两弧交于点D,且点A,点D在BC异侧,连结AD,量一量线段AD的长,约为()
| A.2.5cm | B.3.0cm | C.3.5cm | D.4.0cm |
如图,图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进的方向).其中E为AB的中点,AH>HB,判断三人行进路线长度的大小关系为()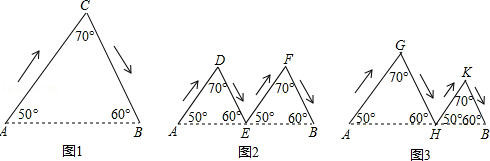
| A.甲<乙<丙 | B.乙<丙<甲 | C.丙<乙<甲 | D.甲=乙=丙 |