如图所示,在长30m,宽20m的花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.要使种植花草的面积为532m2,那么小道进出口的宽度应为多少m?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)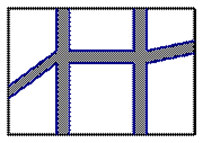
如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,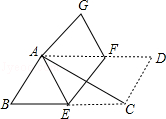
(1)求证:四边形AECF是菱形;
(2)连接AC,若平行四边形ABCD的面积为8,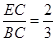 ,求AC•EF的值.
,求AC•EF的值.
先化简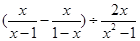 ,然后在-1,0,1,2四个数中选一个合适的代入求值.
,然后在-1,0,1,2四个数中选一个合适的代入求值.
如图,抛物线 与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.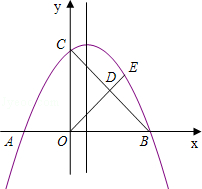
(1)求抛物线的解析式;
(2)作Rt△OBC的高OD,延长OD与抛物线在第一象限内交于点E,求点E的坐标;
(3)①在x轴上方的抛物线上,是否存在一点P,使四边形OBEP是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由;
②在抛物线的对称轴上,是否存在上点Q,使得△BEQ的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
如图,已知反比例函数y= (x>0,k是常数)的图象经过点A(1,4),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(x>0,k是常数)的图象经过点A(1,4),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(1)写出反比例函数解析式;
(2)求证:△ACB∽△NOM;
(3)若△ACB与△NOM的相似比为2,求出B点的坐标及AB所在直线的解析式.
已知:如图,在▱ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.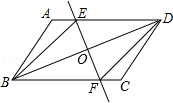
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.