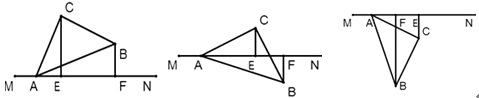
(1)如图1,平面内有一等腰直角三角板ABC(∠ACB=90°)和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,试证明线段AF,BF,CE之间的数量关系为AF+BF=2CE.(提示:过点C做BF的垂线,利用三角形全等证明.)
(2)若三角板绕点A顺时针旋转至图2的位置,其他条件不变,试猜想线段AF、BF、CE之间的数量关系,并证明你的猜想.
(3)若三角板绕点A顺时针旋转至图3的位置,其他条件不变,则线段AF、BF、CE之间的数量关系为 .