如图在△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=90°,将△DCE绕点C旋转(0°<∠ACD<180°),连结BD和AE:
(1)求证:△BCD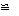 △ACE;
△ACE;
(2)试确定线段BD和AE的数量关系和位置关系;
(1)计算: ;
(2)解不等式组 并把它的解集在数轴(如图)上表示出来.

如图,在 中, , , .点 是 边上的一动点,点 从点 出发以每秒 的速度沿 方向匀速运动,以 为边作等边 (点 、点 在 同侧),设点 运动的时间为 秒, 与 重叠部分的面积为 .
(1)当点 落在 内部时,求此时 与 重叠部分的面积 (用含 的代数式表示,不要求写 的取值范围);
(2)当点 落在 上时,求此时 与 重叠部分的面积 的值;
(3)当点 落在 外部时,求此时 与 重叠部分的面积 (用含 的代数式表示).
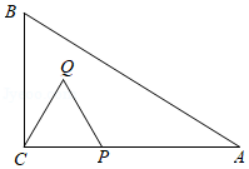
如图,已知 内接于 , 是 的直径, 的平分线交 于点 ,交 于点 ,连接 ,作 ,交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径和 的长.
某快递公司为了提高工作效率,计划购买 、 两种型号的机器人来搬运货物,已知每台 型机器人比每台 型机器人每天多搬运20吨,并且3台 型机器人和2台 型机器人每天共搬运货物460吨.
(1)求每台 型机器人和每台 型机器人每天分别搬运货物多少吨?
(2)每台 型机器人售价3万元,每台 型机器人售价2万元,该公司计划采购 、 两种型号的机器人共20台,必须满足每天搬运的货物不低于1800吨,请根据以上要求,求出 、 两种机器人分别采购多少台时,所需费用最低?最低费用是多少?
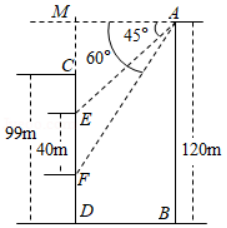
如图,在一座山的前方有一栋住宅,已知山高 ,楼高 ,某天上午9时太阳光线从山顶点 处照射到住宅的点 外.在点 处测得点 的俯角 ,上午10时太阳光线从山顶点 处照射到住宅点 处,在点 处测得点 的俯角 ,已知每层楼的高度为 , ,问:以当天测量数据为依据,不考虑季节天气变化,至少要买该住宅的第几层楼,才能使上午10时太阳光线照射到该层楼的外墙?