如图所示,在空间内有一直角坐标系 ,直线
,直线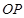 与
与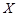 轴正方向夹角为
轴正方向夹角为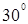 。第一象限内有两个方向均垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线
。第一象限内有两个方向均垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线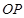 是它们的理想边界,
是它们的理想边界,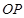 上方区域Ⅰ中磁场的磁感应强度为
上方区域Ⅰ中磁场的磁感应强度为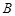 ,在第四象限内有一沿
,在第四象限内有一沿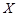 轴负方向的匀强电场。一质量为
轴负方向的匀强电场。一质量为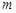 、电荷量为
、电荷量为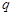 的质子(不计重力及质子对磁场、电场的影响)以速度
的质子(不计重力及质子对磁场、电场的影响)以速度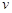 从
从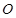 点沿与
点沿与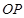 成
成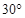 角方向垂直磁场进入区域Ⅰ,质子先后通过磁场区域Ⅰ和Ⅱ后,恰好垂直通过
角方向垂直磁场进入区域Ⅰ,质子先后通过磁场区域Ⅰ和Ⅱ后,恰好垂直通过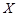 轴上的
轴上的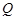 点(未画出)进入第四象限内的匀强电场中,最后从
点(未画出)进入第四象限内的匀强电场中,最后从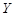 轴上的
轴上的 点与
点与 轴负方向成
轴负方向成 角射出,求:
角射出,求: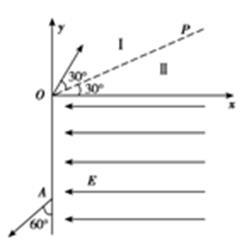
(1)区域Ⅱ中磁场的磁感应强度大小;
(2)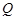 点到
点到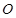 点的距离;
点的距离;
(3)匀强电场的电场强度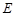 的大小
的大小
下暴雨时,有时会发生山体滑坡或泥石流等地质灾害。某地有一倾角为θ=37°(sin37°="0.6" 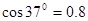 )的山坡C,上面有一质量为2m的石板B,其上下表面与斜坡平行;B上有一碎石堆A(含有大量泥土),A和B均处于静止状态,如图所示。假设某次暴雨中,A浸透雨水后总质量为m(可视为质量不变的滑块),在极短时间内,A、B间的动摩擦因数μ1减小为
)的山坡C,上面有一质量为2m的石板B,其上下表面与斜坡平行;B上有一碎石堆A(含有大量泥土),A和B均处于静止状态,如图所示。假设某次暴雨中,A浸透雨水后总质量为m(可视为质量不变的滑块),在极短时间内,A、B间的动摩擦因数μ1减小为 ,B、C间的动摩擦因数μ2减小为0.5,A、B开始运动。已知A开始运动时,A离B下边缘的距离l=12m,C足够长。取重力加速度大小g=10m/s2。求:
,B、C间的动摩擦因数μ2减小为0.5,A、B开始运动。已知A开始运动时,A离B下边缘的距离l=12m,C足够长。取重力加速度大小g=10m/s2。求: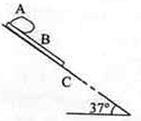
(1)A和B加速度的大小;
(2)A在B上运动的时间
某星球的质量约为地球质量的8倍,半径约为地球半径的2倍。已知地球的第一宇宙速度为7.9 km/s,则航天器在该星球表面附近绕星球做匀速圆周运动的速度大小约为多少?
交管部门为了监测汽车是否按规定的限速行驶,以保安全,在我们学校校门前安装了电子测速仪,来检查是否超过40km/h的限速。其工作原来是:测速仪先后两次发出并接受超声波信号,再根据两次信号的时间差,测出被测车辆的速度。如果某次检测车速时,第一次从发出至接受到超声波信号用了0.4秒,第二次从发出至接收到超声波信号用了0.3秒,两次信号发出的时间间隔是1秒,则被测汽车的速度是多少?是否超速?(假设超声波速度 =340米/秒,且保持不变;发射和接受的声波信号脉冲如监视屏上所示)
=340米/秒,且保持不变;发射和接受的声波信号脉冲如监视屏上所示)

(提示:规范答题和形成良好的解题思路是我们解决物理问题必须具备的良好习惯,对于14题按指定的思路先进行分析,然后规范答题)
兄妹俩为了测量自家的阳台距地面的高度,两人分别拿一个小石子,妹先让小石子自由下落,已知最后2秒的位移是60m,(g取10m/s2)
(1)阳台离地面的高度;
(2)最后1s的平均速度为多少;
(3)若妹释放2s后,兄也从阳台将石子竖直投下,要两石子同时落地,兄给石子多大的向下的初速度.
以 的速度行驶的汽车,制动刹车后做匀减速运动,在
的速度行驶的汽车,制动刹车后做匀减速运动,在 内前进
内前进 .求:
.求:
(1)汽车的加速度;
(2)从汽车开始刹车时计时,5.0 内汽车前进的距离.
内汽车前进的距离.