如图1所示的坐标系内，在x0（x0＞0）处有一垂直工轴放置的挡板．在y轴与挡板之间的区域内存在一个与xoy平珏垂直且指向纸内的匀强磁场，磁感应强度B=0.2T．位于坐标原点O处的粒子源向xoy平面内发射出大量同种带正电的粒子，所有粒子的初速度大小均为vo=1.0×106m/s，方向与x轴正方向的夹角为θ，且0≤θ≤90°．该粒子的比荷为
=1.0×108C/kg，不计粒子所受重力和粒子间的相互作用，粒子打到挡板上后均被挡板吸收．
（1）求粒子在磁场中运动的轨道半径R：
（2）如图2所示，为使沿初速度方向与x轴正方向的夹角θ=30°射出的粒子不打到挡板上，则x0必须满足什么条件？该粒子在磁场中运动的时间是多少？
（3）若x0=5.0×10﹣2m，求粒子打在挡板上的范围（用y坐标表示），并用“
”图样在图3中画出粒子在磁场中所能到达的区域：
如图所示，绷紧的传送带，始终以2 m/s的速度匀速斜向上运行，传送带与水平方向间的夹角θ＝30°。现把质量为10 kg的工件轻轻地放在传送带底端P处，由传送带传送至顶端Q处。已知P、Q之间的距离为4 m，工件与传送带间的动摩擦因数为μ＝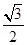
，取g＝10 m/s2。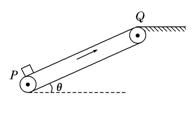
(1)通过计算说明工件在传送带上做什么运动；
(2)求工件从P点运动到Q点所用的时间。
A、B两列火车，在同一轨道上同向行驶，A车在前，其速度vA＝10 m/s，B车在后，其速度vB＝30 m/s，因大雾能见度低，B车在距A车x0＝85 m时才发现前方有A车，这时B车立即刹车，但B车要经过180 m才能停止，问：B车刹车时A车仍按原速率行驶，两车是否会相撞？若会相撞，将在B车刹车后何时相撞？若不会相撞，则两车最近距离是多少？
(10分)如图所示，A、B两物体叠放在水平地面上，已知A、B的质量分别为mA=10kg，mB=20kg，A、B之间，B与地面之间的动摩擦因数为μ=0.5。一轻绳一端系住物体A，另一端系于墙上，绳与竖直方向的夹角为37°今欲用外力将物体B匀速向右拉出，求所加水平力F的大小，并画出A、B的受力分析图。
（取g=10m/s2，sin37°=0.6,cos37°=0.8）
一质量m=0.5kg的滑块以一定的初速度冲上一倾角
=37°足够长的斜面，已知滑块上滑过程中的v
图象如图所示，取sin37°=0.6,cos37°=0.8，g=10m/s2，求：
（1）滑块与斜面间的动摩擦因数；
（2）滑块返回斜面底端时的速度大小。
如图所示，质量为m=1kg木块在拉力F作用下沿水平方向加速运动，加速度a=5.2m/s2。至水平面末端时速度v0=6m/s，此时撤去拉力，木块运动到质量为M=2kg小车上。已知木块与地面、木块与小车动摩擦因素u=0.4，不计小车与地面摩擦。已知拉力与水平方向夹角为53°，g=10m/s2，sin53°=0.8，cos53°=0.6。
求：（1）拉力F大小（2）为使木块不离开小车，小车最短为多长？