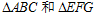是两块完全重合的等边三角形纸片（如图①所示），O是AC（或EF）的中点，
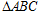不动，将
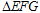绕O点顺时针转
．
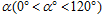（1）试分别说明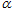
是多少度时，点F在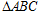外部、BC上、内部（不证明）？
（2）当点F不在BC上时，在图②、图③两种情况下（设EF或延长线与BC交于P，EG与CA或延长线交于Q），分别写出OP与OQ的数量关系，并从图②、③中选一种情况给予证明）．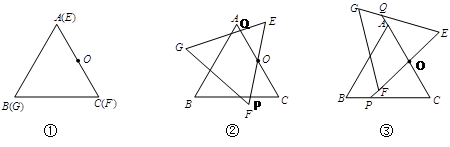
在开展“学雷锋社会实践”活动中，某校为了解全校1200名学生参加活动的情况，随机调查了50名学生每人参加活动的次数，并根据数据绘成条形统计图如下：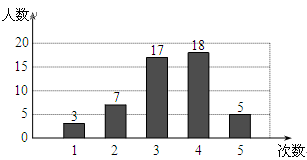
（1）求这50个样本数据的平均数、众数和中位数；
（2）根据样本数据，估算该校1200名学生共参加了多少次活动．
解方程：
．
计算：
一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为
，两车之间的距离为
，图中的折线表示
与
之间的函数关系．
根据图象进行以下探究
（1）请解释图中点
的实际意义；
（2）求慢车和快车的速度；
（3）求线段BC所表示的与之间的函数关系式，并写出自变量的取值范围；
在矩形纸片ABCD中，AB=6，BC=8，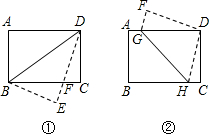
（1）将矩形纸片沿BD折叠，使点A落在点E处（如图①），设DE和BC相交于点F，试说明△BDF为等腰三角形，并求BF的长；
（2）将矩形纸片折叠，使B与D重合（如图②）求折痕GH的长。