某人去水果批发市场采购苹果，他看中了Ａ、Ｂ两家苹果。这两家苹果品质一样，零售价都为6元／千克，批发价各不相同。
Ａ家规定：批发数量不超过1000千克，按零售价的92%优惠；批发数量不超过2000千克，按零售价的90%优惠；超过2000千克的按零售价的88%优惠。
B家的规定如下表：
| 数量范围（千克） |
0～500 |
500以上～1500 |
1500以上～2500 |
2500以上 |
| 价 格（元） |
零售价的95% |
零售价的85% |
零售价的75% |
零售价的70% |
【示例：批发价格分段计算。如：某人在B家批发苹果2100千克，则总费用="6×95%" ×500+6×85%×1000+6×75%×（2100－1500）】
（1）如果他批发600千克苹果，则他在A 家批发需要 元，在B家批发需要
元；
（2）如果他批发
千克苹果（1500＜＜2000），则他在A 家批发需要 元，在B家批发需要 元（用含的代数式表示）；
（3）现在他要批发1800千克苹果，你能帮助他选择在哪家批发更优惠吗?请说明理由。
把两个三角形按如图1放置，其中
，
，
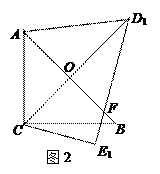
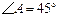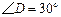，且
，
．把△DCE
绕点C顺时针旋转15°得到△D1CE1，如图2，这时AB与
CD1相交于点
，与D1E1相交于点F．
（1）求
的度数；
（2）求线段AD1的长；
（3）若把△D1CE1绕点
顺时针再旋转30°得到△D2CE2，这时点B在△D2CE2的内部、外部、还是边上？请说明理由．
列方程或方程组解应用题：
2008年5月12日14时28分在我国四川省汶川地区发生了里氏8.0级强烈地震，灾情牵动全国人民的心．“一方有难、八方支援”，某厂计划加工1500顶帐篷支援灾区，在加工了300顶帐篷后，由于情况紧急，该厂又增加了人员进行生产，将工作效率提高到原来的1.5倍，结果提前4天完成任务．问该厂原来每天加工多少顶帐篷．
某校学生会准备调查本校初中三年级同学每天（除课间操外）课外锻炼的平均时间．
（1）确定调查方式时，①甲同学说：“我到1班去调查全体同学”；②乙同学说：“我到体育场上去询问参加锻炼的同学”；③丙同学说：“我到初中三年级每个班去随机调查一定数量的同学”．上面同学说的三种调查方式中最为合理的是___________（填写序号）；
（2）他们采用了最为合理的调查方式收集数据，并绘制出如图1所示的条形统计图和如图2所示的扇形统计图，请将图1补充完整；
（3）若该校初中三年级共有240名同学，则其中每天（除课间操外）课外锻炼平均时间不大于20分钟的人数约为__________人．
(注：图2中相邻两虚线形成的圆心角为30°)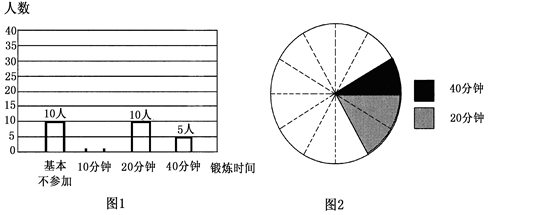
如图，点D是⊙O直径CA的延长线上一点，点B在⊙O上，且AB＝AD＝AO．
（1）求证：BD是⊙O的切线；
（2）若点E是劣弧BC上一点，弦AE与BC相交
于点F，且CF＝9，cos∠BFA＝
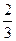，求EF的长．
如图1，矩形纸片ABCD中，AB＝4，BC＝4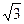
，将矩形纸片沿对角线AC向下翻折，点D落在点D’处，联结B D’，如图2，求线段BD’ 的长．