如图所示，顶角θ＝45°的金属导轨MON固定在水平面内，导轨处在方向竖直向下、磁感应强度为B的匀强磁场中．一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向右滑动，导体棒的质量为m，导轨与导体棒单位长度的电阻均为r.导体棒与导轨接触点为a和b，导体棒在滑动过程中始终保持与导轨良好接触．t＝0时导体棒位于顶角O处，则流过导体棒的电流强度I、导体棒内产生的焦耳热Q、导体棒做匀速直线运动时水平外力F、导体棒的电功率P各量大小随时间变化的关系正确的是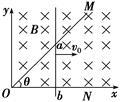
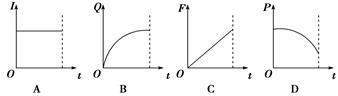
如图所示，边长为L的正方形导线框abcd，质量为m、电阻为R，垂直纸面向外的匀强磁场区域宽度为H（H>L），磁感应强度为B. 线框竖直上抛，线框ab边向上离开磁场时的速率是进入磁场时速率的一半，线框离开磁场后继续上升一段高度，然后落下并匀速进入磁场．不计空气阻力，整个运动过程中线框不转动.求线框向上
（1）ab边离开磁场时的速率；
（2）通过磁场过程中安培力所做的功；
（3）完全进入磁场过程中所通过横截面的电荷量．
如图所示，圆形区域存在磁感应强度大小为B，方向垂直纸面向里的匀强磁场，一电荷量为q，质量为m的粒子沿平行于直径AC的方向射入磁场，射入点到直径AC的距离为磁场区域半径的一半，粒子从D点射出磁场时的速率为
，不计粒子的重力.求
（1）粒子在磁场中加速度的大小；
（2）粒子在磁场中运动的时间；
（3）圆形区域中匀强磁场的半径.
如图所示，光滑绝缘水平桌面上的A、B、C三点是等腰直角三角形的三个顶点，AD为三角形的高，∠BAC＝90°，BC＝0.8m，空间存在方向与BC平行的匀强电场．将质量为
、电荷量为
的小球由A点移到B点，电势能增加
．求：
（1）匀强电场的场强大小；
（2）A、B两点间的电势差UAB；
（3）将小球从B处静止释放，运动到C处时的动能.
如图所示，某同学用插针法测定半圆形玻璃砖的折射率，按规范先后插入
、
、
、
四枚大头针后，移开玻璃砖作出分析图．用圆规以
点为圆心画一个圆，分别交入射光线和折射光线于A点和B点，量出这两点到
轴的距离分别为
、
，求:
①玻璃砖的折射率；
②恰好发生全反射时临界角的正弦值．
近年来，国际热核聚变实验堆计划取得了重大进展，它利用的核反应方程是
.若
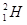和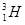
迎面碰撞，初速度大小分别为v1、v2. 、、
、
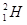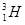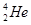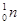的质量分别为m1、m2、m3、m4，反应后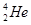的速度大小为v3，方向与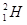的运动方向相同．求中子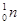的速度(选取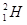的运动方向为正方向，不计释放的光子动量，不考虑相对论效应)．