同向运动的甲乙两质点在某时刻恰好通过同一路标,以此时为计时起点,此后甲质点的速度随时间的变化关系为v=4t+12(m/s),乙质点位移随时间的变化关系为x=2t+4t2(m),试求:
(1)两质点何时再次相遇;
(2)两质点相遇之前何时相距最远的距离.
带负电的小物体A放在倾角为θ(sinθ=0.6)的绝缘斜面上,整个斜面处于范围足够大、方向水平向右的匀强电场中,如图所示。物体A的质量为m、电量为-q,与斜面间的动摩擦因数为μ,它在电场中受到的电场力的大小等于重力的一半。物体A在斜面上由静止开始下滑,经时间t后突然在斜面区域加上范围足够大的匀强磁场,磁场方向与电场强度方向垂直,磁感应强度大小为B,此后物体A沿斜面继续下滑距离L后离开斜面。重力加速度为g。求:
(1)物体A在斜面上的运动情况?说明理由。
(2)加磁场前A沿斜面运动的距离为多少?
(3)物体A在斜面上运动过程中有多少能量转化为内能?(结果用字母表示)
有一质量为m的卫星以轨道半径为r、周期为T环绕某行星做圆轨道运动,已知引力常量为G。求:
(1)行星的质量M;
(2)作用于卫星上的引力F;
(3)若行星的半径是卫星轨道半径的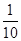 ,行星表面的重力加速度g是多大?
,行星表面的重力加速度g是多大?
如图所示,竖直悬挂的弹簧测力计吊一物体,处于静止状态,弹簧测力计示数表示物体对弹簧的拉力,其大小为F,试论证物体受到重力大小等于F,每一步推导都要写出所根据的物理规律。
如图所示,一带电粒子以某一速度在竖直平面内做直线运动,经过一段时间后进入一垂直于纸面向里、磁感应强度为B的最小的圆形匀强磁场区域(图中未画出磁场区域),粒子飞出磁场后垂直电场方向进入宽为L的匀强电场。电场强度大小为E,方向竖直向上。当粒子穿出电场时速度大小变为原来的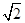 倍。已知带电粒子的质量为m,电量为g,重力不计。粒子进入磁场前的速度如图与水平方向成θ=60°角。求:
倍。已知带电粒子的质量为m,电量为g,重力不计。粒子进入磁场前的速度如图与水平方向成θ=60°角。求: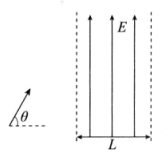
(1)粒子带什么性质的电荷;
(2)粒子在磁场中运动时速度多大;
(3)该最小的圆形磁场区域的面积为多大?
10只相同的轮子并排水平排列,圆心分别为O1、O2、O3…O10,已知O1O10=3.6m,水平转轴通过圆心,轮子均绕轴以n=±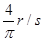 的转速顺时针转动。现将一根长0.8m、质量为2.0kg的匀质木板平放在这些轮子的左侧,木板左端恰好与O1竖直对齐(如图所示),木板与轮子间的动摩擦因数为0.16,不计轴与轮间的摩擦,g取10m/s2。求:
的转速顺时针转动。现将一根长0.8m、质量为2.0kg的匀质木板平放在这些轮子的左侧,木板左端恰好与O1竖直对齐(如图所示),木板与轮子间的动摩擦因数为0.16,不计轴与轮间的摩擦,g取10m/s2。求: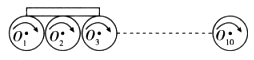
(1)木板在轮子上水平移动的总时间;
(2)轮子由于传送木板所多消耗的能量。