在边长为2的正方形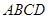 中,
中,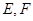 分别是
分别是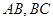 的中点,沿
的中点,沿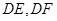 以及
以及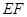 把
把
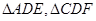 和
和 都向上折起,使
都向上折起,使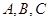 三点重合,设重合后的点为
三点重合,设重合后的点为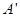 ,那么对于四面体
,那么对于四面体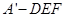 中的下列命题:
中的下列命题:
①点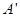 在平面
在平面 上的射影是
上的射影是 的垂心;
的垂心;
②四面体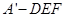 的外接球的表面积是
的外接球的表面积是 .
.
③在线段 上存在一点
上存在一点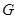 ,使得直线
,使得直线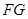 与直线
与直线 所成的角是
所成的角是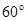 ;
;
其中正确命题的序号是 .
下面是高考第一批录取的一份志愿表:
| 志愿 |
学校 |
专业 |
|
| 第一志愿 |
1 |
第1专业 |
第2专业 |
| 第二志愿 |
2 |
第1专业 |
第2专业 |
| 第三志愿 |
3 |
第1专业 |
第2专业 |
现有4所重点院校,每所院校有3 个专业是你较为满意的选择,如果表格填满且规定学校没有重复,同一学校的专业也没有重复的话,你将有不同的填写方法的种数是。
已知方程x2- ( 1 - i )x + m + 2i = 0有实根,若m Î R,求m= 。
在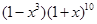 的展开中,
的展开中, 的系数是。
的系数是。
已知| z | =1,则| z-3+4i |的最大值=_____________。
从1,3,5,7中任取2个数字,从0,2,4,6,8中任取2个数字,组成没有重复数字的四位数,其中能被5整除的四位数共有个.(用数字作答)