如图,在 中,
中, ,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为()
,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为()
A.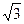 B.
B. C.
C. D.
D.

球面上有三点,其中任意两点的球面距离都等于球的大圆周长的 ,经过这三点的小圆的周长为
,经过这三点的小圆的周长为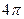 ,则这个球的表面积为()
,则这个球的表面积为()
A. |
B. |
C. |
D.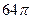 |
若 满足
满足 ,则使得
,则使得 的值最小的
的值最小的 是()
是()
| A.(4.5,3) | B.(3,6) | C.(9,2) | D.(6,4) |
设函数
 ,若
,若 ,则
,则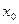 的取值范围是()
的取值范围是()
A.(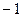 ,1) ,1) |
B.(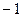 , ,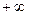 ) ) |
C.(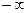 , ,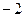 ) ) (0, (0,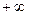 ) ) |
D.(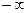 , ,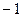 ) ) (1, (1,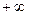 ) ) |
过抛物线y =4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是()
=4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是()
A.y =2x-1 =2x-1 |
B.y =2x-2 =2x-2 |
C.y =-2x+1 =-2x+1 |
D.y =-2x+2 =-2x+2 |