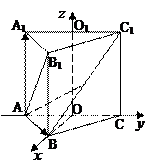如图,四棱锥 中,底面ABCD为菱形,且
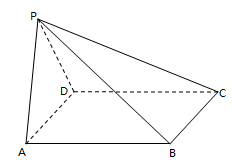
中,底面ABCD为菱形,且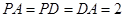 ,
, .
.
(1)求证: ;
;
(2)若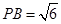 ,求点C到平面PBD的距离.
,求点C到平面PBD的距离.
试比较1.70.2 、log2.1 0.9与0.82.1的大小关系,并按照从小到大的顺序排列为
0.9与0.82.1的大小关系,并按照从小到大的顺序排列为
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A—DC— B。
B。
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角E—DF—C的余弦值;
(3)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.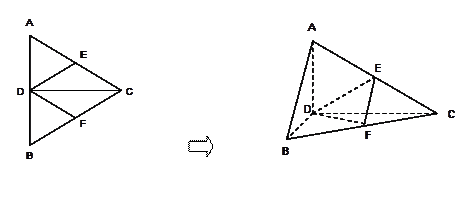
如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.
(1)求证:平面EBD⊥平面SAC;
(2)设SA=4,AB=2,求点A到平面SBD的距离;
如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;
(3)求三棱锥C-BGF的体积.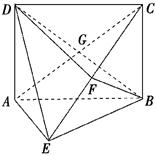
已知正三棱柱ABC—A1B1C1,底面边长AB=2,AB1⊥BC1,点O、O1分别是边AC,A1C1的中点,建立如图所示的空间直角坐标系.
⑴求正三棱柱的侧棱长.
⑵若M为BC1的中点,试用基向量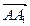 、
、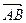 、
、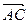 表示向量
表示向量 ;
;
⑶求异面直线AB1与BC所成角的余弦值.