下列说法正确的是（）①试验条件不会影响某事件出现的频率；②在-优题课

下列说法正确的是（）
①试验条件不会影响某事件出现的频率；
②在相同的条件下试验次数越多，就越有可能得到较精确的估计值，但各人所得的值不一定相同；
③如果一枚骰子的质量分布均匀，那么抛掷后每个点数出现的机会均等；
④抛掷两枚质量分布均匀的相同的硬币，出现“两个正面”、“两个反面”、“一正一反”的机会相同．

A．①②

B．②③

C．③④

D．①③

科目数学题型选择题难度中等

知识点：利用频率估计概率

关于 $x$ 的一元一次不等式 $x ﹣ 3 \geq 0$ 的解集在数轴上表示为（　　）

A．		B．
C．		D．

如图是《九章算术》中“堑堵”的立体图形，它的左视图为（　　）

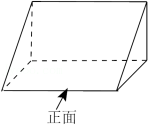
A．		B．
C．		D．

下表是2022年1月﹣5月遵义市 $P M_{2.5}$ （空气中直径小于等于 $2.5$ 微米的颗粒）的平均值，这组数据的众数是（　　）

月份	1月	2月	3月	4月	5月
$P M_{2.5}$ （单位： $μ g / m^{3}$ ）	$24$	$23$	$24$	$25$	$22$

$22$

$23$

$24$

$25$

全国统一规定的交通事故报警电话是（　　）

$122$

$110$

$120$

$114$

已知二次函数 $y ＝ a x^{2} + b x + c （ a ＞ 0 ）$ ．

（1）若 $a ＝ 1 ， b ＝ 3$ ，且该二次函数的图象过点 $（ 1 ， 1 ）$ ，求c的值；

（2）如图所示，在平面直角坐标系xOy中，该二次函数的图象与x轴相交于不同的两点 $A （ x_{1}, 0 ）$ 、 $B （ x_{2}, 0 ）$ ，其中 $x_{1} ＜ 0 ＜ x_{2}$ 、 $| x_{1} | ＞ | x_{2} |$ ，且该二次函数的图象的顶点在矩形 $A B F E$ 的边 $E F$ 上，其对称轴与 $x$ 轴、 $B E$ 分别交于点 $M 、 N ， B E$ 与 $y$ 轴相交于点 $P$ ，且满足 $\tan ∠ A B E = \frac{3}{4}$ ．

①求关于 $x$ 的一元二次方程 $a x^{2} + b x + c ＝ 0$ 的根的判别式的值；

②若 $N P ＝ 2 B P$ ，令 $T = \frac{1}{a^{2}} + \frac{16}{5} c$ ，求 $T$ 的最小值．

阅读材料：十六世纪的法国数学家弗朗索瓦•韦达发现了一元二次方程的根与系数之间的关系，可表述为“当判别式 $Δ \geq 0$ 时，关于 $x$ 的一元二次方程 $a x^{2} + b x + c ＝ 0 （ a \neq 0 ）$ 的两个根 $x_{1} 、 x_{2}$ 有如下关系： $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} x_{2} = \frac{c}{a}$ ”．此关系通常被称为“韦达定理”．