初步探索 感悟方法
如图1，用水平线和竖直线将平面分成若干个边长为1的小正方形格子，小正方形的顶点，叫格点，以格点为顶点的多边形叫格点多边形，设格点多边形的面积为S，它各边上格点的个数和为x．
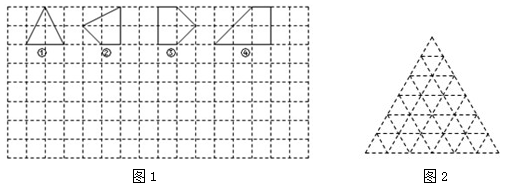
（1）如图1中所示的格点多边形，其内部都只有一个格点，它们的面积与各边上格点的个数和的对应关系如下表，请填写下表并写出S与x之间的关系式，答：S= ．
| 多边形的序号 |
① |
② |
③ |
④ |
… |
| 多边形的面积S |
2 |
|
3 |
|
… |
| 各边上格点的个数和x |
4 |
5 |
6 |
|
… |
（2）你可以画些格点多边形，使这些多边形内部都有而且只有2个格点．
此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S= ．
（3）请你继续探索，当格点多边形内部有且只有n（n是正整数）个格点时，猜想S与x、n之间的关系式S= ．（用含有字母x、n的代数式表示）
积累经验 拓展延伸
如图2，对等边三角形网格中的类似问题进行探究：等边三角形网格中每个小等边三角形的面积为1，小等边三角形的顶点为格点，以格点为顶点的多边形称为格点多边形．
（4）设格点多边形的面积为S，它各边上格点的个数和为x，当格点多边形内部有且只有n个格点时，猜想S与x、n之间的关系式S= ．（用含有字母x、n的代数式表示）
解不等式组：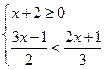
，并写出该不等式组的最小整数解.
解方程组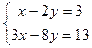
解方程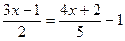 
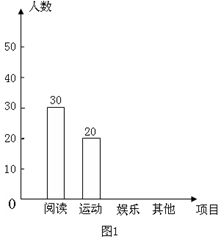
某中学为了了解该校学生的课余活动情况，从阅读、运动、娱乐、其他等四个方面调查了若干名学生的兴趣爱好，并将调查结果绘制了如下两幅不完整的统计图（图1，图2），请你根据统计图中提供的信息解答下列问题：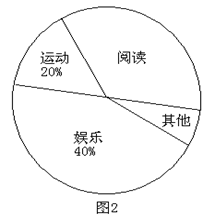
（1）在这次研究中，一共调查了多少名学生？
（2）“其他”在扇形统计图中所占的圆心角是多少度？
（3）补全条形统计图．
 |
某班组织春游，A、B两个风景点全班每人任选一处。去A风景点的每人付费25元，去B风景点的每人付费35元。若去B风景点的人数比去A风景点的少4人，全班共付费1660元。问全班有多少人？
解：设去A风景点的学生有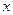
人，则全班有（）人，
根据题意，得
解这个方程，得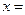 
∴
答：全班有人。