观察下列等式：
12×231=132×21，
13×341=143×31，
23×352=253×32，
34×473=374×43，
62×286=682×26，
……
以上每个等式中两边数字是分别对称的，且每个等式中组成两位数与三位数的数字之间具有相同规律，我们称这类等式为“数字对称等式”．
（1）根据上述各式反映的规律填空，使式子成为“数字对称等式”：
①52× ＝ ×25；
② ×396＝693× ．
（2）设这类等式左边两位数的十位数字为
，个位数字为
，且2≤
≤9，写出表示“数字对称等式”一般规律的式子（含、），并说明理由．
用橡皮泥做一个棱长为4cm的正方体．
（1）如图（1），在顶面中心位置处从上到下打一个边长为1cm的正方体通孔，打孔后的橡皮泥的表面积为 cm2；
（2）如果在第（1）题打孔后，再在正面中心位置处（按图（2）中的虚线）从前到后打一个边长为1cm的正方体通孔，那么打孔后的橡皮泥的表面积为 cm2；
（3）如果把第（2）题中从前到后所打的正方形通孔扩大成一个长xcm、宽1cm的长方形通孔，能不能使所得橡皮泥的表面积为130cm2？如果能，请求出x；如果不能，请说明理由．
如图是某市民健身广场的平面示意图，它是由6个正方形拼成的长方形，已知中间最小的正方形A的边长是1米，
（1）若设图中最大正方形B的边长是x米，请用含x的代数式分别表示出正方形F、E和C的边长；
（2）观察图形的特点可知，长方形相对的两边是相等的（如图中的MN和PQ）．请根据这个等量关系，求出x的值；
（3）现沿着长方形广场的四条边铺设下水管道，由甲、乙2个工程队单独铺设分别需要10天、15天完成．如果两队从同一点开始，沿相反的方向同时施工2天后，因甲队另有任务，余下的工程由乙队单独施工，试问还要多少天完成？
我市城市居民用电收费方式有以下两种：
（甲）普通电价：全天0.53元/度；
（乙）峰谷电价：峰时（早8：00～晚21：00）0.56元/度；谷时（晚21：00～早8：00）0.36元/度．
已知小明家下月计划总用电量为400度，
（1）若其中峰时电量为100度，则小明家按照哪种方式付电费比较合适？能省多少元？
（2）峰时电量为多少度时，两种方式所付的电费相等？
“*”是新规定的这样一种运算法则：a*b=a2+2ab
（1）试求2*（﹣1）的值；
（2）若（﹣2）*（1*x）=x+9，求x的值．
关于x的方程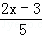
=
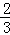x﹣3与方程3n﹣1=3（x+n）﹣2n的解互为相反数，求n的值．