如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A(-1,5),B(-1,0),C(-4,3).

(1)画出△ABC关于y轴对称的△A1B1C1;(其中A1、B1、C1是A、B、C的对应点,不写画法)
(2)写出A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.
如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点.
(1)若BK=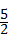 KC,求
KC,求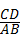 的值;
的值;
(2)连接BE,若BE平分∠ABC,则当AE=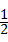 AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE=
AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE=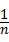 AD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
AD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.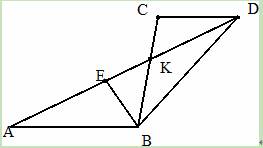
如图,已知反比例函数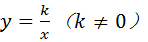 的图象经过点(
的图象经过点(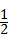 ,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).
,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P,连接0P、OQ,求△OPQ的面积.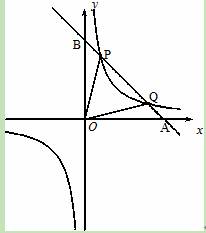
某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容.规定:每位考生先在三个笔试题(题签分别用代码B1、B2、B3表示)中抽取一个,再在三个上机题(题签分别用代码J1、J2、J3表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地各抽取一个题签.
(1)用树状图或列表法表示出所有可能的结构;
(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“B1”的下表为“1”)均为奇数的概率.
如图,在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶.在航行到B处时,发现灯塔A在我军舰的正北方向500米处;当该军舰从B处向正西方向行驶至达C处时,发现灯塔A在我军舰的北偏东60°的方向.求该军舰行驶的路程.(计算过程和结果均不取近似值)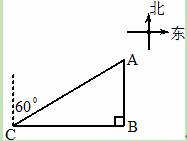
(1)计算: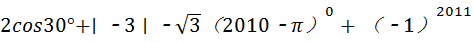 .
.
(2)解不等式组: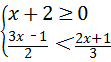 ,并写出该不等式组的最小整数解.
,并写出该不等式组的最小整数解.