如图,直线y=kx-2与x轴交于点B,直线y=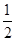 x+1与y轴交于点C,这两条直线交于点A(2,a).
x+1与y轴交于点C,这两条直线交于点A(2,a).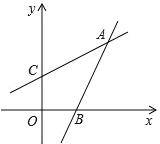
(1)直接写出a的值;
(2)求点B,C的坐标及直线AB的表达式;
(3)求四边形ABOC的面积.
如图所示,点O在直线AB上,OE平分∠COD,且∠AOC︰∠COD︰∠DOB=1︰3︰2,求∠AOE的度数.
如图所示,直线AB、CD分别交EF于点G、H,若∠2=∠3,∠1=50°,求∠4的度数.
如图,⊙M与x轴交于A、B两点,其坐标分别为 、
、 ,直径CD⊥x轴于N,抛物线
,直径CD⊥x轴于N,抛物线 经过A、B、D三点,
经过A、B、D三点,
(1)求m的值及点D的坐标.
(2)若直线CE切⊙M于点C,G在直线CE上,已知点G的横坐标为3.求G的纵坐标
(3)对于(2)中的G,是否存在过点G的直线,使它与(1)中抛物线只有一个交点,请说明理由.
(4)对于(2)中的G直线FG切⊙M于点F,求直线DF的解析式.
如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=3,另两边与反比例函数的图象分别相交于点E,F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
(1)该反比例函数的解析式是什么?
(2)当四边形AEGF为正方形时,点F的坐标时多少?
(3)阅读合作学习内容,请解答其中的问题;
小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”
针对小亮提出的问题,请你判断这两个矩形能否全等?直接写出结论即可;这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,
其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1.
(1)画出△A1OB1;
(2)在旋转过程中点B所经过的路径长为(直接写答案);
(3)求在旋转过程中线段AB ,OB扫过的图形的面积和.