勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
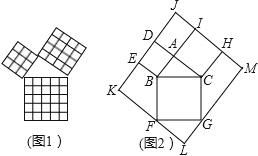
| A.90 | B.100 | C.110 | D.121 |
如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,则△ABC的面积等于△BEF的面积的 ( )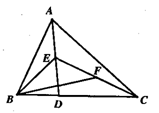
A.2倍B.3倍C.4倍D.5倍
下面有两个对代数式进行变形的过程:
(1)(c+b)(c-b)-a(a+2b)=c2-b2-a2-2ab=c2-(b2+a2+2ab)=c2-(a+b)2;
(2)(2a2+2)(a2-1)=2(a2+1)(a2-1)=2(a4-1).
其中,完成“分解因式”要求的是 ( )
| A.只有(1) | B.只有(2) | C.有(1)和(2) | D.一个也没有 |
如图,已知AB∥CD,则∠α、∠β和∠γ之间的关系为 ( )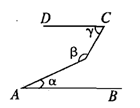
| A.β+γ-α=180° | B.α+γ=β |
| C.α+β+γ=360° | D.α+β-2γ=180° |
下列命题中,属于真命题的是 ( )
| A.如果a>b,那么a-2<b-2. |
| B.任何数的零次幂都等于1. |
| C.两条直线被第三条直线所截,同旁内角互补. |
| D.平移不改变图形的形状和大小. |
一个不等式组的解集在数轴上表示出来如图所示,则下列符合条件的不等式组为( )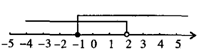
A.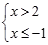 |
B.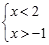 |
C.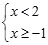 |
D.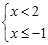 |