如图,已知在Rt△ABC中,∠ACB=90°,AC=6,BC=8,BE平分∠ABC交AC于点E,EF⊥AB,垂足为F.
(1)求EF的长度;
(2)作CD⊥AB,垂足为D,CD与BE相交于G,试说明:CE=CG
我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称_______,___;
(2)如图,已知格点(小正方形的顶点) ,
,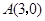 ,
,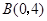 ,请你直接写出所有以格点为顶点,
,请你直接写出所有以格点为顶点, 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形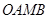 的顶点M的坐标。
的顶点M的坐标。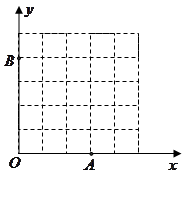
(3)如图,将 绕顶点
绕顶点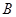 按顺时针方向旋转
按顺时针方向旋转 ,得到
,得到 ,连结
,连结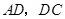 ,
,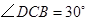 .求证:
.求证: ,即四边形
,即四边形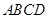 是勾股四边形.
是勾股四边形.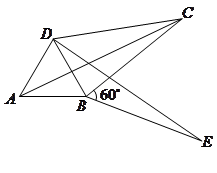
某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。 求:(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?(2)每件衬衫降价多少元时,商场平均每天赢利最多?
如图,已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120º,BD=10.
(1)求证:CA=CD;(2)求⊙O的半径.
一商店1月份的利润是2500元,3月份的利润达到3025元,这两个月的利润平均月增长的百分率是多少?
不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为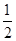 .
.
(1)试求袋中蓝球的个数.
(2)第一次任意摸一个(不放回),第二次再摸一个球,请用画树形图或表格法,求两次摸到都是白球的概率。