如甲图所示,水平光滑地面上用两颗钉子(质量忽略不计)固定停放着一辆质量为M=2kg的小车,小车的四分之一圆弧轨道是光滑的,半径为R=0.6m,在最低点B与水平轨道BC相切,视为质点的质量为m=1kg的物块从A点正上方距A点高为h=1.2m处无初速下落,恰好落入小车圆弧轨道滑动,然后沿水平轨道滑行恰好停在轨道末端C。现去掉钉子(水平面依然光滑未被破坏)不固定小车,而让其左侧靠在竖直墙壁上,该物块仍从原高度处无初速下落,如乙图所示。不考虑空气阻力和物块落入圆弧轨道时的能量损失,已知物块与水平轨道BC间的动摩擦因数为μ=0.1,重力加速度g取10 m/s2,求: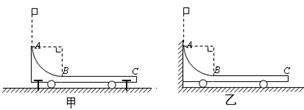
(1)水平轨道BC长度;
(2)小车不固定时物块再次与小车相对静止时距小车B点的距离;
(3)两种情况下由于摩擦系统产生的热量之比.
如图所示为高速摄影机拍摄到的子弹穿透苹果瞬间的照片。该照片经放大后分析出,在曝光时间内,子弹影像前后错开的距离约为子弹长度的1%~2%。已知子弹飞行速度约为500 m/s,由此可估算出这幅照片的曝光时间大约是多少?
子弹穿过苹果图
一质点在x轴上只朝着x轴的正方向运动,各个时刻的位置坐标如下表,则此质点开始运动后:
| t/s |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
| x/m |
2 |
4 |
6 |
8 |
8 |
8 |
12 |
16 |
20 |
24 |
(1)质点在前10 s内的位移、路程各为多大?
(2)质点在8 s末的瞬时速度为多大?
(3)质点在0到18 s这段时间内的平均速度为多大?
如图所示,一辆轿车从超市出发,向东行驶了300 m到达电影院,继续行驶了150 m到达度假村,又向西行驶了950 m到达博物馆,最后回到超市,以超市所在的位置为原点,以向东的方向为正方向,用1个单位长度表示100 m,试求:
(1)在直线坐标系上表示出超市、电影院、度假村和博物馆的位置;
(2)轿车从电影院经度假村到博物馆的位移与路程分别为多少?
在图中时间轴上标出第2 s末、第5 s末、第2 s、第4 s,并说明它们表示的是时间还是时刻。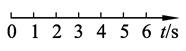
第16届亚运会于2010年11月12日在广州开幕,火炬传递在广东省内21个地级以上城市举行。观察图中的旗帜和甲、乙两火炬手所传递的火炬的火焰,则甲、乙两火炬手相对于静止旗杆的运动情况如何?