已知函数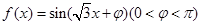 ,
, 为
为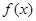 的导函数,若
的导函数,若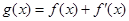 为奇函数,求
为奇函数,求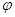 的值.
的值.
已知函数 ,
(Ⅰ)证明:当
;
(Ⅱ)证明:当
时,存在
,使得对
(Ⅲ)确定
的所以可能取值,使得存在
,对任意的
恒有
.
已知函数
的图像是由函数
的图像经如下变换得到:先将
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
个单位长度.
(Ⅰ)求函数
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于
的方程
在
内有两个不同的解
.
(1)求实数
的取值范围;
(2)证明:
已知椭圆
过点
,且离心率为
.
(Ⅰ)求椭圆
的方程;
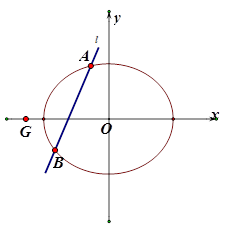
(Ⅱ)设直线
交椭圆
于
两点,判断点
与以线段
为直径的圆的位置关系,并说明理由.
如图,在几何体
中,四边形
是矩形,
平面
,
,
,
分别是线段
的中点.
(Ⅰ)求证:
平面
;
(Ⅱ)求平面
与平面
所成锐二面角的余弦值.
某银行规定,一张银行卡若在一天内出现3次密码尝试错误,该银行卡将被锁定,小王到银行取钱时,发现自己忘记了银行卡的密码,但是可以确定该银行卡的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试.若密码正确,则结束尝试;否则继续尝试,直至该银行卡被锁定.
(Ⅰ)求当天小王的该银行卡被锁定的概率;
(Ⅱ)设当天小王用该银行卡尝试密码次数为
,求
的分布列和数学期望.