如图,点O为坐标原点,点A(1,1).若函数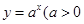 且
且 及
及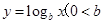 且
且 的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )
的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )

A. |
B.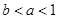 |
C. |
D.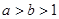 |
已知 和
和 是两条不同的直线,
是两条不同的直线,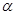 和
和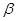 是两个不重合的平面,那么下面给出的条件中一定能推出
是两个不重合的平面,那么下面给出的条件中一定能推出
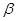 的是()
的是()
A. ,且 ,且 |
B. ∥ ∥ ,且 ,且 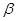 |
C. ,且 ,且 ∥ ∥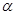 |
D.  ,且 ,且 ∥ ∥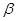 |
已知双曲线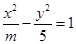 (
(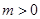 )的右焦点与抛物线
)的右焦点与抛物线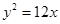 的焦点相同,则此双曲线的离心率为()
的焦点相同,则此双曲线的离心率为()
A.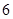 |
B.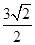 |
C.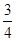 |
D.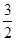 |
已知点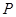 在抛物线
在抛物线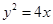 上,则点
上,则点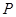 到直线
到直线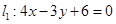 的距离和到直线
的距离和到直线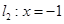 的距离之和的最小值为()
的距离之和的最小值为()
A. |
B.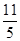 |
C. |
D.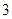 |
如图,直三棱柱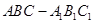 侧面
侧面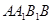 是边长为5的正方形,
是边长为5的正方形,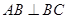 ,
,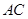 与
与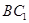 成
成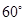 角,则
角,则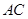 长()
长()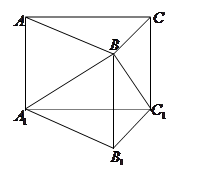
| A.13 | B.10 | C.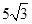 |
D. |
关于直线a,b,c以及平面M,N,给出下面命题:
①若a//M,b//M, 则a//b②若a//M, b⊥M,则b⊥a③若a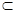 M,b
M,b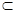 M,且c⊥a,c⊥b,则c⊥M④若a⊥M, a//N,则M⊥N,其中正确命题的个数为()
M,且c⊥a,c⊥b,则c⊥M④若a⊥M, a//N,则M⊥N,其中正确命题的个数为()
| A.0个 | B.1个 | C.2个 | D.3个 |