如图所示，用一块长
的木板在墙和桌面间架设斜面，桌面长
。斜面与水平桌面的倾角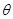
可在0~60°间调节后固定。将质量m=0.6kg的小物块从斜面顶端静止释放，物块与斜面间的动摩擦因数
0.5，物块与桌面间的动摩擦因数
，忽略物块在斜面与桌面交接处的速度大小变化。（重力加速度取
；最大静摩擦力等于滑动摩擦力）
（1）求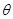角增大到多少时，物块能从斜面开始下滑；（用正切值表示）
（2）当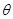增大到37°时，物块恰能停在桌面边缘，求物块与桌面间的动摩擦因数（已知sin37°=0.6，cos37°=0.8）
（3）继续增大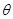角，当=53°时，是否还能停在桌面上？如果能，求物块距桌面右边缘的距离，如果不能，，求物块离开桌面右边缘时的速度大小？
分把质量是2.0×10－3 kg的带电小球B用细线悬挂起来，如图所示．若将带电荷量为4.0×10－8 C的小球A靠近B，平衡时细线与竖直方向成45°角，A、B在同一水平面上，相距0.30 m，试求：
(1)A球受到的电场力多大？
(2)B球所带电荷量为多少？
“电子能量分析器”主要由处于真空中的电子偏转器和探测板组成．偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成，A、B为电势值不等的等势面，其过球心的截面如图所示．一束电荷量为E、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射，进入偏转电场区域，最后到达偏转器右端的探测板N，其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间．忽略电场的边缘效应．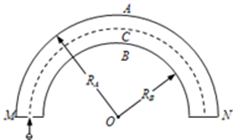
（1）判断球面A、B的电势高低，并说明理由；
（2）求等势面C所在处电场强度E的大小；
（3）若半球面A、B和等势面C的电势分别为φA、φB和φC，则到达N板左、右边缘处的电子，经过偏转电场前、后的动能改变量△Ek左和△Ek右分别为多少？
（4）比较|△Ek左|和|△Ek右|的大小，并说明理由．
如图所示，平行板电容器的两个极板A、B分别接在电压为60V的恒压源上，两板间距为3cm，电容器带电荷量为6×10-8 C，A极板接地．求：
（1）平行板电容器的电容；
（2）平行板电容器两板之间的电场强度；
（3）距B板为2cm的C点处的电势；
（4）将一个电荷量为q=8×10-9 C的正点电荷从B板移到A板电场力所做的功．
如图所示，Q为固定的正点电荷，A、B两点在Q的正上方和 Q相距分别为 h和0.25h，将另一点电荷从 A点由静止释放，运动到B点时速度正好又变为零．若此电荷在A点处的加速度大小为
，试求：
（1）此电荷在B点处的加速度．
（2）A、B两点间的电势差（用Q和h表示）
如图所示，一条长为L的绝缘细线，上端固定，下端系一质量为m的带电小球，将它置于电场强度为E、方向水平向右的匀强电场中，当小球平衡时，悬线与竖直方向的夹角为45°．
（1）小球带何种电荷？电荷量为多少？
（2）若将小球向左拉至悬线成水平位置，然后由静止释放小球，则放手后小球做什么运动？经多长时间到达最低点．