一个电子以v0＝4×107m/s的速度，方向与电场方向相同，射入电场强度E＝2×105V/m的匀强电场中，如图所示，已知电子电量e＝－1.6×10－19C，电子质量m＝9.1×10－31kg.试求：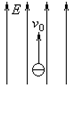
（1）从电子的入射点到达速度为0之点的两点间电势差是多少? 两点间距离是多少?
（2）电子到达速度为0之前所需的时间是多少?
如图所示为质谱仪上的原理图，M为粒子加速器，电压为U1=5000V；N为速度选择器，磁场与电场正交，磁感应强度为B1=0.2T，板间距离为d=0.06m；P为一个边长为l的正方形abcd的磁场区，磁感应强度为B2=0.1T，方向垂直纸面向外，其中dc的中点S开有小孔，外侧紧贴dc放置一块荧光屏．今有一比荷为
=108C/kg的正离子从静止开始经加速后，恰好通过速度选择器，从a孔以平行于ab方向进入abcd磁场区，正离子刚好经过小孔S 打在荧光屏上．求：
（1）粒子离开加速器时的速度v；
（2）速度选择器的电压U2；
（3）正方形abcd边长l．
如图所示，一矩形线圈在匀强磁场中绕OO′轴匀速转动，磁场方向与转轴垂直，磁场的磁感应强度为B．线圈匝数为n，电阻为r，长为l1，宽为l2，转动角速度为ω．线圈两端外接阻值为R的电阻和一个理想交流电流表．求：
（1）线圈转至图示位置时的感应电动势；
（2）电流表的读数；
（3）从图示位置开始计时，感应电动势的瞬时值表达式．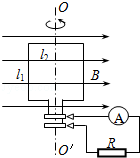
如图（甲）所示，MN、PQ为水平放置的足够长的平行光滑导轨，导轨间距L为0.5m，导轨左端连接一个阻值为2Ω的定值电阻R，将一根质量为0.2kg的金属棒cd垂直放置在导轨上，且与导轨接触良好，金属棒cd的电阻r=2Ω，导轨电阻不计，整个装置处于垂直导轨平面向下的匀强磁场中，磁感应强度B=2T．若棒以1m/s的初速度向右运动，同时对棒施加水平向右的拉力F作用，并保持拉力的功率恒为4W，从此时开始计时，经过2s金属棒的速度稳定不变，图（乙）为安培力与时间的关系图象．试求：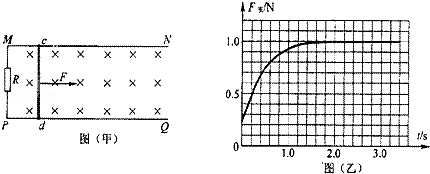
（1）金属棒的最大速度；
（2）金属棒的速度为3m/s时的加速度；
（3）求从开始计时起2s内电阻R上产生的电热．
如图所示，在平面直角坐标系xoy的第四象限有垂直纸面向里的匀强磁场，一质量为m=5.0×10﹣8kg、电量为q=1.0×10﹣6C的带电粒子，从静止开始经U0=10V的电压加速后，从P点沿图示方向进入磁场，已知OP=30cm，（粒子重力不计，sin37°=0.6，cos37°=0.8），求：
（1）带电粒子到达P点时速度v的大小
（2）若磁感应强度B=2.0T，粒子从x轴上的Q点离开磁场，求QO的距离
（3）若粒子不能进入x轴上方，求磁感应强度B'满足的条件．
如图所示，在倾角θ=37°的斜面上，固定着宽L=0.20m的平行金属导轨，在导轨上端接有电源和滑动变阻器，已知电源电动势E=6.0V，内电阻r=0.50Ω．一根质量m=10g的金属棒ab放在导轨上，与两导轨垂直并接触良好，导轨和金属棒的电阻忽略不计．整个装置处于磁感应强度B=0.50T、垂直于轨道平面向上的匀强磁场中．若金属导轨是光滑的，已知sin37°=0.6，cos37°=0.8，取g=10m/s2，求：
（1）要保持金属棒静止在导轨上，滑动变阻器接入电路的阻值是多大？
（2）金属棒静止在导轨上时，如果使匀强磁场的方向瞬间变为竖直向上，则此时导体棒的加速度是多大？