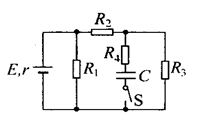
如图所示,水平绝缘轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接,半圆形轨道的半径R=0.40m。轨道所在空间存在水平向右的匀强电场,电场强度E=1.0×104N/C。现有一电荷量q=+1.0×10-4C,质量m=0.10kg的带电体(可视为质点),在水平轨道上的P点由静止释放,带电体运动到圆形轨道最低点B时的速度vB=5.0m/s。已知带电体与水平轨道间的动摩擦因数μ=0.50,重力加速度g=l0m/s2。求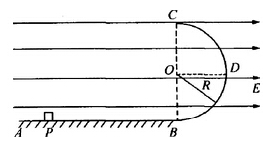
(1)带电体在水平轨道上的释放点P到B点的距离;
(2)带电体第一次经过C点时的速度。
如图所示,在xoy坐标系第一象限内有匀强磁场,磁场区域上边界刚好与直线y=a重合,磁感应强度为B。一个带正电的离子在坐标为(a,0)的A点以某一速度进入磁场区域,进入磁场时速度方向与x轴正向夹角为30°,离子质量为m,带电量为q。不计离子重力。
(1)若离子离开磁场时位置坐标为(a,a)的C点,求离子运动的速度大小
(2)当离子进入磁场的速度满足什么条件时可使离子在磁场区域运动的时间最长?并求出最长时间是多少?
如图,质量m=5×10-8 kg的带电粒子以v0="2" m/s的速度从水平放置的平行金属板A、B中央飞入电场,已知板长L="10" cm,板间距离d="2" cm,当AB间加电压UAB=1.0×103 V时,带电粒子恰好沿直线穿过电场(设此时A板电势比B板电势高)。g=10m/s2。求: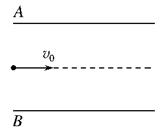
(1)带电粒子的电性,电荷量为多少?
(2)A、B间所加电压在什么范围内带电粒子能从板间飞出?
如图甲所示,一个圆形线圈的匝数n=1000,线圈面积S=200cm2,线圈的电阻r="1" Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间的变化规律如图乙所示。求: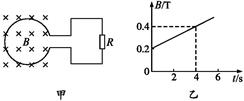
(1)前4s内的感应电动势;
(2)前4s内通过R的电荷量;
(3)线圈电阻r消耗的功率。
如图所示,水平放置的平行金属导轨,相距l=0.50m,左端接一电阻R="0.20" Ω,磁感应强度B=0.40T的匀强磁场方向垂直于导轨平面,导体棒ab垂直放在导轨上,并能无摩擦地沿导轨滑动,导轨和导体棒的电阻均可忽略不计,当ab以v=4.0m/s的速度水平向右匀速滑动时,求: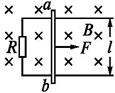
(1)ab棒中感应电动势的大小;
(2)回路中感应电流的大小;
(3)维持ab棒做匀速运动的水平外力F的大小
如图所示的电路中,电源的电动势E=3.0 V,内阻r=1.0Ω;电阻R1=10 Ω,R2=10 Ω,R3=30 Ω,R4=35 Ω;电容器的电容C=100μF.电容器原来不带电,求接通电键S后R3两端的电压和流过R4的总电量.