足够长光滑斜面BC的倾角α=53°，小物块与水平面间的动摩擦因数μ=0.5，水平面与斜面之间B点有一小段弧形连接，一质量m=2kg的小物块静止于A点，现在AB段对小物块施加与水平方向成α=53°角的恒力F作用，如图（a）所示，小物块在AB段运动的速度--时间图像如图（b）所示，到达B点迅速撤去恒力F．（已知sin53°=0.8，cos53°=0.6，g取10m/s2），求：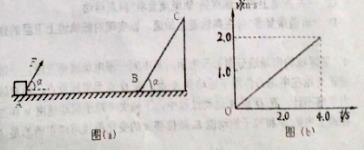
（1）小物块所受到的恒力F；
（2）小物块从B点沿斜面向上运动，到返回B点所用的时间；
（3）小物块能否返回到A点?若能，计算小物块通过A点时的速度：若不能，计算小物块停止运动时离B点的距离。
质量m=1.5kg的物块（可视为质点）在水平恒力Ｆ作用下，从水平面上Ａ点静止开始运动，运动一段距离撤去该力，物块继续滑行t=2.0s停在B点，已知A、B两点的距离x=5.0m，物块与水平面间的动摩擦因数
，求恒力F多大？
．(2012·扬州模拟)如图所示，一根劲度系数k＝200 N/m的轻质弹簧拉着质量为m＝0.2 kg的物体从静止开始沿倾角为θ＝37°的斜面匀加速上升，此时弹簧伸长量x＝0.9 cm，在t＝1.0 s内物体前进了s＝0.5 m。
求：(1)物体加速度的大小；
(2)物体和斜面间的动摩擦因数。(取g＝10 m/s2，sin37°＝0.6，cos37°＝0.8)
静止在水平地面上的木块，质量为m=10kg，受水平恒力F作用一段时间后撤去该恒力，物体运动的速度时间图像如图所示，求：
（1）物体6秒的位移和两段加速度分别是多少
（2）F的大小
（3）木块与地面间的动摩擦因素µ
如图所示，一质量为m、电荷量为q、重力不计的微粒，从倾斜放置的平行电容器I的A板处由静止释放，A、B间电压为U1。微粒经加速后，从D板左边缘进入一水平放置的平行板电容器II，由C板右边缘且平行于极板方向射出，已知电容器II的板长为板间距离的2倍。电容器右侧竖直面MN与PQ之间的足够大空间中存在着水平向右的匀强磁场（图中未画出），MN与PQ之间的距离为L，磁感应强度大小为B，在微粒的运动路径上有一厚度不计的窄塑料板（垂直纸面方向的宽度很小），斜放在MN与PQ之间，
=45°。求：
（1）微粒从电容器I加速后的速度大小；
（2）电容器IICD间的电压；
（3）假设粒子与塑料板碰撞后，电量和速度大小不变、方向变化遵循光的反射定律，碰撞时间极短忽略不计，微粒在MN与PQ之间运动的时间和路程。
如图甲所示，平行金属导轨竖直放置，导轨间距为L＝1m，上端接有电阻R1＝3
，下端接有电阻R2＝6，虚线OO′下方是垂直于导轨平面的匀强磁场．现将质量m＝0.1 kg、电阻不计的金属杆ab，从OO′上方某处垂直导轨由静止释放，杆下落0.2 m过程中始终与导轨保持良好接触，加速度a与下落距离h的关系图象如图乙所示. 求：
（1）磁感应强度B；（2）杆下落0.2 m过程中通过金属杆的电荷量q.