如图,⊙O的半径OC=5cm,直线l⊥OC,垂足为H,且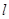 交⊙O于A、B两点,AB=8cm,则l沿OC所在直线平移后与⊙O相切,则平移的距离是( )
交⊙O于A、B两点,AB=8cm,则l沿OC所在直线平移后与⊙O相切,则平移的距离是( )

A.1cm B.2cm C.8cm D.2cm或8cm
某种商品若按标价的八折出售,可获利20%,若按原价出售可获利
| A.25% | B.40% | C.50% | D.66.7% |
已知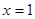 是关于
是关于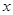 的方程
的方程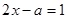 的解,则
的解,则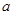 的值是
的值是
A.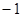 |
B.1 | C. |
D.3 |
某中学冬季进行体育锻炼,举行跳绳和踢毽比赛,该校七年一班准备购买6根绳和10个毽,已知绳比毽的单价少2元,班长算了一下,他们共需要36元钱。如果设绳的单价为 元,那么下列方程正确的是
元,那么下列方程正确的是
A.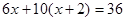 |
B.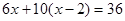 |
C. |
D. |
如图,OC,OD分别是∠AOB,∠BOC的平分线,且∠COD=35°,则∠AOB的度数是
| A.100° | B.120° | C.140° | D.150° |
为了解某初中学校学生的视力情况,需要抽取部分学生进行调查,下列抽取学生的方法最合适的是
| A.随机抽取该校一个班级的学生 |
| B.随机抽取该校一个年级的学生 |
| C.随机抽取该校一部分男生 |
| D.分别从该校七、八、九年级中各班随机抽取10%的学生 |