某同学报名参加校运动会,有以下5个项目可供选择:
径赛项目:100m,200m,400m(分别用A1、A2、A3表示);
田赛项目:跳远,跳高(分别用B1、B2表示).
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率为多少?
(2)该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
如图,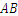 是⊙O的一条弦,
是⊙O的一条弦,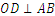 ,垂足为C,交⊙O于点D,点E在⊙O上.
,垂足为C,交⊙O于点D,点E在⊙O上.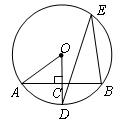
(1)若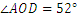 ,求
,求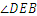 的度数;
的度数;
(2)若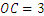 ,
,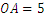 ,求
,求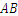 的长.
的长.
如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的距离是11m。试以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系,求题中抛物线的函数表达式.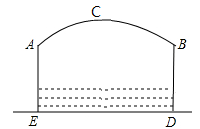
已知反比例函数 .
.
(1)画出该函数的大致图象。
(2)这个函数的大致图象位于哪些象限?函数值y随自变量x的增大如何变化?
解下列方程
(1)
(2)
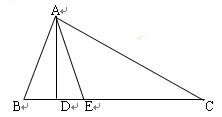
如图,在△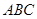 中,∠
中,∠ >∠
>∠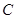 ,
, ,
, 平分∠
平分∠ .
.
(1)若∠ =70°,∠
=70°,∠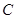 =30°.
=30°.
①求∠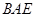 =°;②∠
=°;②∠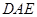 =°.
=°.
(2)探究:小明认为如果只要知道∠ -∠
-∠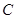 =n°,就能求出∠
=n°,就能求出∠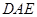 的度数?请你就这个问题展开探究:
的度数?请你就这个问题展开探究:
①实验:填表
∠ 的度数 的度数 |
∠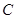 的度数 的度数 |
∠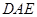 的度数 的度数 |
| 70° |
30° |
(此格不需填写) |
| 65° |
25° |
|
| 50° |
20° |
|
| 80° |
56° |
②结论:当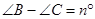 时,试用含
时,试用含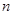 的代数式表示∠
的代数式表示∠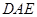 的度数,并写出推导过程;
的度数,并写出推导过程;
③应用:若∠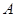 =56°,∠
=56°,∠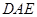 =12°,则∠
=12°,则∠ =°.
=°.