函数 的图象大致是( )
的图象大致是( )
A. |
B. |
C. |
D. |
定义在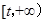 上的函数
上的函数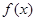 ,
, 单调递增,
单调递增,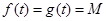 ,若对任意
,若对任意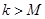 ,存在
,存在 ,
,
使得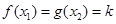 成立,则称
成立,则称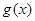 是
是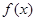 在
在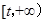 上的“追逐函数”.已知
上的“追逐函数”.已知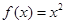 ,下列四个函数:
,下列四个函数:
①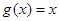 ;②
;②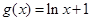 ;③
;③ ;④
;④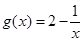 .其中是
.其中是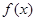 在
在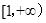 上的“追逐函数”
上的“追逐函数”
的有
A.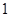 个 个 |
B.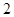 个 个 |
C.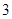 个 个 |
D. 个 个 |
如图所示的程序框图的功能是求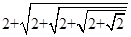 的值,则框图中的①、②两处应
的值,则框图中的①、②两处应
分别填写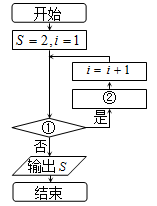
A.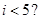 , ,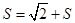 |
B.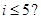 , ,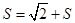 |
C.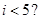 , ,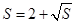 |
D.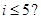 , ,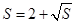 |
.已知双曲线的中心在原点,焦点在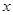 轴上,若其渐近线与圆
轴上,若其渐近线与圆 相切,则
相切,则
此双曲线的离心率等于
A.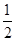 |
B.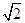 |
C. |
D.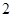 |
.将函数 的图象向右平移
的图象向右平移 个单位,得到的图象关于原点对称,则
个单位,得到的图象关于原点对称,则 的
的
最小正值为
A. |
B. |
C. |
D. |
已知某路口最高限速 ,电子监控测得连续
,电子监控测得连续 辆汽车的速度如图的茎叶图(单位:
辆汽车的速度如图的茎叶图(单位: ).若从中任取
).若从中任取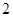 辆,则恰好有
辆,则恰好有 辆汽车超速的概率为
辆汽车超速的概率为
A.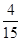 |
B. |
C. |
D.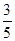 |