下列说法中：
①如果两个三角形可以依据“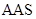
”来判定全等，那么一定也可以依据“
”
来判定它们全等；
②如果两个三角形都和第三个三角形不全等，那么这两个三角形也一定不全等；
③要判断两个三角形全等，给出的条件中至少要有一组边对应相等．
正确的是
| A．①和② | B．②和③ | C．①和③ | D．①②③ |
在九年级体育中考中，某校某班参加仰卧起坐测试的一组女生（每组8人）测试成绩如下（单位：次/分）：44，45，42，48，46，43，47，45．则这组数据的极差为（ ）
| A．2 | B．4 |
| C．6 | D．8 |
衢州市“十二五”规划纲要指出，力争到2015年，全市农民人均年纯收入超13000元，数13000用科学记数法可以表示为（ ）
| A．13×103 | B．1.3×104 |
| C．0.13×104 | D．130×102 |
数﹣2的相反数为（ ）
| A．2 | B． |
| C．﹣2 | D． |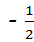
如图，西安路与南京路平行，并且与八一街垂直，曙光路与环城路垂直．如果小明站在南京路与八一街的交叉口，准备去书店，按图中的街道行走，最近的路程约为（ ）
| A． | B． | ||
| C． | D． |
如图，在平面直角坐标系中，过格点A，B，C作一圆弧，点B与下列格点的连线中，能够与该圆弧相切的是（ ）
| A．点（0，3） | B．点（2，3） |
| C．点（5，1） | D．点（6，1） |