虚线MN下方有竖直向上的匀强电场,场强大小E=2×103V/m,MN上方有一竖直长为L=0.5m的轻质绝缘杆,杆的上下两端分别固定一带电小球A、B(可看成质点),质量均为m=0.01kg,A带电量为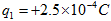 ;B带电量
;B带电量 ,B到MN的距离h=0.05m。现将杆由静止释放(g取10m/s2),求:
,B到MN的距离h=0.05m。现将杆由静止释放(g取10m/s2),求:
(1)小球B在匀强电场中,而A还未进入电场时,两小球的加速度大小。
(2)从开始运动到A刚要进入匀强电场过程的时间。
如图所示,竖直平面内放一直角杆AOB,杆的水平部分粗糙,动摩擦因数为0.20,杆的竖直部分光滑,两部分各套有质量分别为2.0kg和1.0kg的小球A和B,A、B间用细绳相连,初始位置OA=1.5m,OB=2.0m,g=10m/s2。 
(1)若用水平拉力F1沿杆缓慢拉A,使之移动0.5m,则在该过程中
①小球A受到的摩擦力多大?
②小球A、B和地球组成的系统机械能的变化量多大?
(2)若小球A、B都有一定的初速度,A在水平拉力F2的作用下,使B由初始位置以1.2m/s的速度匀速上升0.5m,此过程中F2做的功?(绳子始终处于绷紧状态)
一密封盒B放置在水平面上,密封盒与水平面间的动摩擦因数μ=0.5,密封盒的内表面光滑,在内表面上有一小球A靠左侧壁放置,此时小球A与密封盒的右侧壁相距为l,如图所示。A、B的质量均为m。现对密封盒B施加一个大小等于2mg(g为重力加速度)、方向水平向右的推力F,使B和A一起从静止开始向右运动,当密封盒B运动的距离为d时,立刻将推力撤去,此后A和B发生相对运动,再经一段时间球A碰到盒的右侧壁。 求
(1)在推力F作用的过程中盒子的左侧壁对小球A做的功;
(2)球A相对于盒从左侧壁运动至右侧壁所经过的时间t并说明此时l与d之间的关系。
在半径为R=12000km的某星球表面, 宇航员做了如下实验,实验装置如图所示。竖直面内的光滑轨道有轨道AB和圆轨道BC组成,将质量为m=0.1kg的小球,从轨道AB上高H处的某点静止滑下,用力传感器测出小球经过C点是对轨道的压力F,改变H的大小,可测出相应的F大小,F随H的变化关系如图乙所示,求:
(1)圆轨道的半径;
(2)该星球表面的重力加速度大小;
(3)该星球的第一宇宙速度。
如图所示,一倾角为 的足够长固定光滑斜面底端有一与斜面垂直的挡板M,物块A、B之间用一与斜面平行的轻质弹簧连接且静止在斜面上。现用外力沿斜面向下缓慢推动物块B,当弹簧具有5J的弹性势能时撤去推力,释放物块B 。已知物块A、B的质量分别为5kg和10kg,弹簧的弹性势能的表达式为
的足够长固定光滑斜面底端有一与斜面垂直的挡板M,物块A、B之间用一与斜面平行的轻质弹簧连接且静止在斜面上。现用外力沿斜面向下缓慢推动物块B,当弹簧具有5J的弹性势能时撤去推力,释放物块B 。已知物块A、B的质量分别为5kg和10kg,弹簧的弹性势能的表达式为 ,其中弹簧的劲度系数为k=1000N/m,x为弹簧的形变量,g=10m/s2。求
,其中弹簧的劲度系数为k=1000N/m,x为弹簧的形变量,g=10m/s2。求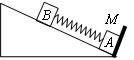
(1)撤掉外力时,物块B的加速度大小;
(2)外力在推动物块B的过程中所做的功;
(3)试判断物块A能否离开挡板M?若A能离开挡板M,求出物块A刚离开挡板M时,物块B的动能;若A不能离开挡板M,求出物块A与挡板M之间的最小作用力。
如图所示,倾角为θ的粗糙斜面的底端有一凹形小滑块,在底端竖直线上离底端高度为H处有一个小球,小球以一定的水平速度v0抛出。
(1)要使小球垂直打在斜面上,试推导小球离斜面底端的高度H与小球速度v0之间的关系。
(2)若斜面倾角θ=37°,凹形小滑块的质量m=1kg,小滑块与斜面间的动摩擦因数μ=0.25。现小滑块以某一初速度从斜面底端上滑,同时在斜面底端正上方的小球以初速度3m/s水平抛出,经过一段时间,小球恰好垂直斜面方向落入凹槽,此时,小滑块还在上滑过程中。求小滑块运动的时间和小滑块的动能变化量。(已知sin37°=0.6, cos37°=0.8, g取10m/s2)