如图，在8×8网格纸中，每个小正方形的边长都为1．
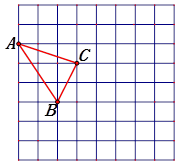
（1）请在网格纸中建立平面直角坐标系，使点A、C的坐标分别为（－4，4），（－1，3），并写出点B的坐标为 ；
（2）画出△ABC关于y轴的对称图形△A1B1C1，并写出B1点的坐标；
（3）在y轴上求作一点P，使△PAB的周长最小，并直接写出点P的坐标．
小明家要在卫生间墙壁（AB）上安装一个淋浴装置．要求淋浴头放至插槽中正常情况下使用时，水不能喷洒到对面墙壁（MN）上，小明经过研究和测量，将其简化成下面的问题：已知淋浴头放入插槽后，喷射最远的水线DE与CD的夹角∠CDE=87°，CD=0．2m，∠BCD=45°，两墙壁之间的距离为2m．请计算插槽安装的最大高度AC．（结果精确到0．1米，参考数据：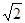
≈1．41，tan48°≈1．11，tan42°≈0．90）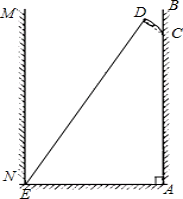
如图所示，在△ABC中，∠C=90°，点D、E分别在AC、AB上，BD平分∠ABC，DE⊥AB，AE=6，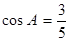
．
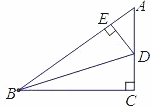
求：（1）DE、CD的长；（2）tan∠DBC的值。
已知关于x的方程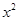
+ax+a-2=0．
（1）若该方程的一个根为1，求a的值及该方程的另一根；
（2）求证：不论a取何实数，该方程都有两个不相等的实数根．
如图，D是△ABC外一点，E是BC边上一点，∠1=∠2，∠3=∠4．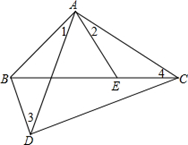
（1）写出图中两对相似三角形（不得添加字母和线）；
（2）请分别说明两对三角形相似的理由．
用适当的方法解下列方程
（1）x2-10x+9=0
（2）（x+2）（x-5）=1