已知三角形 的三个顶点是
的三个顶点是 .
.
(1)求 边上的高所在直线的方程;
边上的高所在直线的方程;
(2)求 边上的中线所在直线的方程
边上的中线所在直线的方程
现有甲、乙两个靶。某射手向甲靶射击一次,命中的概率为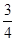 ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ,每命中一次得2分,没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。
,每命中一次得2分,没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。
(Ⅰ)求该射手恰好命中一次的概率;
(Ⅱ)求该射手的总得分X的分布列及数学期望EX.
数列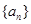 中,
中,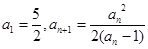
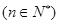 ,用数学归纳法证明:
,用数学归纳法证明: 。
。
在一次购物抽奖活动中,假设某10张奖券中有一等奖卷1张,可获价值50元的奖品;有二等奖卷3张,每张可获价值10元的奖品;其余6张没有奖。某顾客从这10张中任抽2张,求:(1)该顾客中奖的概率;(2)该顾客获得的奖品总价值X(元)的分布列和数学期望。
已知函数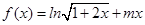 .
.
(Ⅰ)若 为定义域上的单调增函数,求实数
为定义域上的单调增函数,求实数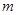 的取值范围;
的取值范围;
(Ⅱ)当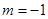 时,求函数
时,求函数 的最大值;
的最大值;
(Ⅲ)当 时,且
时,且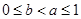 ,证明:
,证明: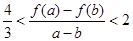 .
.
已知两定点E(-2,0),F(2,0),动点P满足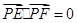 ,由点P向x轴作垂线段PQ,垂足为Q,点M满足
,由点P向x轴作垂线段PQ,垂足为Q,点M满足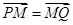 ,点M的轨迹为C.
,点M的轨迹为C.
(1)求曲线C的方程
(2)过点D(0,-2)作直线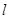 与曲线C交于A、B两点,点N满足
与曲线C交于A、B两点,点N满足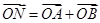
(O为原点),求四边形OANB面积的最大值,并求此时的直线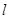 的方程.
的方程.