如图，正方形网格中每一个小正方形的边长都为1，每一个小格的顶点叫做格点．以格点为顶点分别按下列要求画三角形：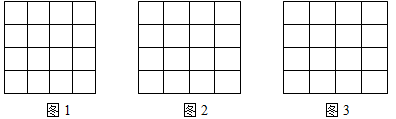
（1）在图1中，画一个三角形，使它的边长都是有理数；
（2）在图2、图3中分别画一个直角三角形，使它们的边长都是无理数，并且要求两个三角形不全等．
下列是小朋友用火柴棒拼出的一列图形：
仔细观察，找出规律，解答下列各题：
（1）第四个图中共有________根火柴，第六个图中共有_________根火柴；
（2）按照这样的规律，第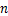
个图形中共有_________根火柴（用含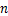的代数式表示）；
（3）按照这样的规律，第2 012个图形中共有多少根火柴？
一杯饮料，第一次倒去一半，第二次倒去剩下的一半……如此倒下去，第五次后剩下饮料是原来的几分之几？第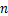
次后呢？
某地电话拨号入网有两种收费方式，用户可以任选其一：
（Ⅰ）计时制：0.05元/分；
（Ⅱ）包月制：50元/月（限一部个人住宅电话上网）．此外，每一种上网方式都得加收通信费0.02元/分．
（1）某用户某月上网的时间为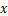
小时，请你分别写出两种收费方式下该用户应该支付的费用；
（2）若某用户估计一个月内上网的时间为20小时，你认为采用哪种方式较为合算？
某班10名学生在一次数学测验中的成绩以90分为标准，超过的分数记为正数，不足的分数记为负数，记录如下：
－7，－10，＋9，＋2，－1，＋5，－8，＋10，＋4，＋9.
（1）最高分和最低分各是多少?
（2）求他们的平均成绩.
先化简，再求值：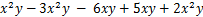
，其中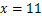
，
.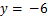