(本小题满分14分)
(1) 证明:当 时,不等式
时,不等式 成立;
成立;
(2) 要使上述不等式 成立,能否将条件“
成立,能否将条件“ ”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由;
”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由;
(3)请你根据⑴、⑵的证明,试写出一个类似的更为一般的结论,且给予证明.
(本小题满分14分)
已知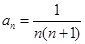 ,数列
,数列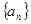 的前
的前 项的和记为
项的和记为 .
.
(1) 求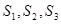 的值,猜想
的值,猜想 的表达式;
的表达式;
(2) 请用数学归纳法证明你的猜想.
(本小题满分14分)
已知 的展开式中所有项的系数和是243.
的展开式中所有项的系数和是243.
(1) 求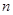 值,并求展开式中二项式系数最大的项;
值,并求展开式中二项式系数最大的项;
(2) 求 值.
值.
(本小题满分14分)
已知: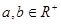 , 求证:
, 求证: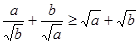 .
.
(本小题满分12分)
有3个男生,2个女生站成一排.
(1)两个女生不站在一起的排法;
(2)男生甲不站两端的排法;
(3)甲、乙之间有且只有一人的排法.