在一个不透明的袋中装有2个黄球，3个黑球和5个红球，它们除颜色外其他都相同．
（1）将袋中的球摇均匀后，求从袋中随机摸出一个球是黄球的概率；
（2）现在再将若干个红球放入袋中，与原来的10个球均匀混合在一起，使从袋中随机摸出一个球是红球的概率是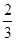
，请求出后来放入袋中的红球的个数．
如图所示，分别过△ABC的顶点A，B，C作对边BC，AC，AB的平行线，交点分别为E，F，D．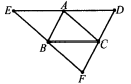
（1）请找出图中所有的平行四边形；
（2）求证：BC=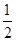
DE．
如图所示，已知点E，F在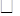
ABCD的对角线BD上，且BE=DF．
求证：（1）△ABE≌△CDF；（2）AE∥CF．
如图所示，已知在△ABC中，AB=AC=5，BC=6，将△ABC沿BC所在直线向右平移6个单位，得到△DCE，连结AD．
（1）请找出图中所有的平行四边形．（2）求四边形ABED的面积．
如图所示，在
ABCD中，DE⊥AB于E，DF⊥BC于F，若∠A=55°，求∠EDF的度数．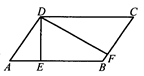
如图所示，在
ABCD中，点E，F分别在BC，AD上，AE∥CF，求证：∠AFC=∠AEC．