如图，抛物线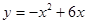
与x轴交于O，A两点，与直线y=2x交于O，B两点．点P在线段OA上以每秒1个单位的速度从点O向终点A运动，作EP⊥x轴交直线OB于E；同时在线段OA上有另一个动点Q，以每秒1个单位的速度从点A向点O运动（不与点O重合）．作CQ⊥x轴交抛物线于点C，以线段CQ为斜边作如图所示的等腰直角△CQD ．设运动时间为t秒．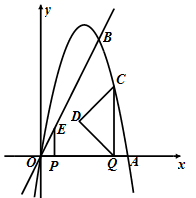
（1）求点B的坐标；
（2）当t =1秒时，求CQ的长；
（3）求t为何值时，点E恰好落在△CQD的某一边所在的直线上；
如图，在△ABC中，AB=AC，点D在BC上，DE∥AC，交AB与点E，点F在AC上，DC=DF，若BC=3，EB=4，CD=x，CF=y，求y与x的函数关系式，并写出自变量x的取值范围．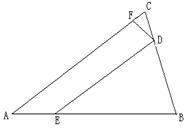
如图，有一段斜坡
长为10米，坡角
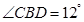，为方便残疾人的轮椅车通行，现准备把坡角降为5°．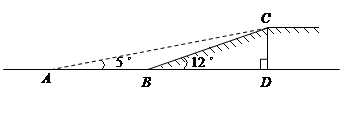 
（1）求坡高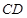
；
（2）求斜坡新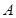起点
与原起点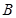
的距离（精确到0．1米）．
如图，已知△ABC中CE⊥AB于E，BF⊥AC于F，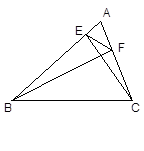
（1）求证：△AFE∽△ABC；
（2）若∠A=60°时 ，求△AFE与△ABC面积之比．
已知抛物线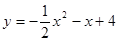
，
（1）用配方法确定它的顶点坐标、对称轴；
（2）
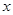取何值时，
随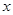增大而减小？
（3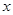）取何值时，抛物线在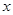轴上方？
在△ABC中，AB=AC=5，BC=6，求cosB、sinA．