如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的小环,小环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d。现将小环从与定滑轮等高的A处由静止释放,当小环沿直杆下滑距离也为d时(图中B处),下列说法正确的是(重力加速度为g)。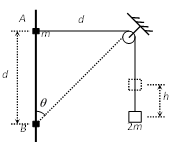
| A.小环刚释放时轻绳中的张力一定大于2mg |
| B.小环到达B处时,重物上升的高度约为0.4d |
C.小环在B处的速度与重物上升的速度大小之比等于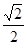 |
| D.小环在从A到B的过程中重力势能减少了mgh |
某游乐场开发了一个名为“翻天滚地”的游乐项目。原理图如图所示:一个3/4圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,地面与圆心O等高,MN 是放在水平地面上长为3R、厚度不计的减振垫,左端M正好位于A点.让游客进入一个中空的透明弹性球,人和球的总质量为m,球的直径略小于圆管直径。将球(内装有参与者)从A处管口正上方某处由静止释放后,游客将经历一个“翻天滚地”的刺激过程。不考虑空气阻力。那么以下说法中错误的是
A.要使球能从C点射出后能打到垫子上,则球经过C点时的速度至少为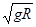 |
B.要使球能从C点射出后能打到垫子上,则球经过C点时的速度至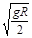 |
C.若球从C点射出后恰好能打到垫子的M端,则球经过C点时对管的作用力大小为 |
D.要使球能通过C点落到垫子上,球离A点的最大高度是 |
设想某登月飞船贴近月球表面绕月球做匀速圆周运动,测得其运动周期为T.飞船在月球上着陆后,航天员利用一摆长为L的单摆做简谐运动,测得单摆振动周期为T0,已知引力常量为G.根据上述已知条件,可以估算的物理量有
| A.月球的质量 | B.飞船的质量 | C.月球到地球的距离 | D.月球的自转周期 |
卡文迪许用扭秤测出引力常量G,被称为第一个“称”出地球质量的人。若已知地球表面的重力加速度g、地球的半径R、地球绕太阳运转的周期T,忽略地球自转的影响,则关于地球质量M,下列计算正确的是
A. |
B. |
C. |
D. |
太阳系外行星大多不适宜人类居住,绕恒星“Glicsc581”运行的行星“Gl-581c”却很值得我们期待。该行星的温度在 到
到 之间,质量是地球的6倍,直径是地球的1.5倍。公转周期为13个地球日。“Glicsc581”的质量是太阳质量的0.31倍。设该行星与地球均视为质量分布均匀的球体,绕其中心天体做匀速圆周运动,则
之间,质量是地球的6倍,直径是地球的1.5倍。公转周期为13个地球日。“Glicsc581”的质量是太阳质量的0.31倍。设该行星与地球均视为质量分布均匀的球体,绕其中心天体做匀速圆周运动,则
| A.在该行星和地球上发射卫星的第一宇宙速度相同 |
B.如果人到了该行星,其体重是地球上的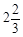 倍 倍 |
C.该行星与“Glicsc581”的距离是日地距离的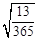 倍 倍 |
D.恒星“Glicsc581”的密度是地球的 倍 倍 |
在空间中水平面MN的下方存在竖直向下的匀强电场,质量为m的带电小球由MN上方的A点以一定初速度水平抛出,从B点进入电场,到达C点时速度方向恰好水平,A、B、C三点在同一直线上,且AB=2BC,如图所示.由此可知( )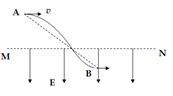
A.电场力为3mg
B.小球带正电
C.小球从A到B与从B到C的运动时间相等
D.小球从A到B与从B到C的速度变化量相等