阅读理解:“分割、拼凑法”是几何证明中常用的方法。苏科版八上数学第一章《全等三角形》中,有以下两道题,其中问题1中的图1分割成两个全等三角形,而问题2是“HL定理”的证明,却将图2两个直角三角形拼成了一个等腰三角形图3.
请按照上面的思路,补全问题1、2的解答:
问题1:已知:如图1,在△ABC中,AB=AC.求证:∠B=∠C.
问题2:如图2,在△ABC和△A1B1C1中,∠C=∠C1=90°,AB=A1B1,AC=A1C1.
求证:△ABC≌△A1B1C1(补全证明过程) .
证明:把两个直角三角形如图3所示拼在一起.
仿照上面的方法解答问题:
问题3:如图4,△ABC中,∠ACB=90°,四边形CDEF是正方形,AE=5,BE=3.
求阴影部分的面积和.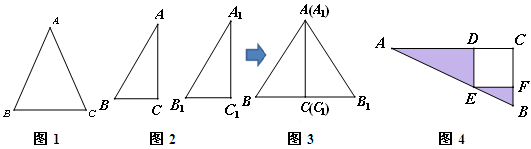
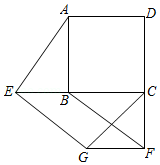
如图, , 分别是正方形 的边 , 延长线上的点,且 ,过点 作 ,交正方形外角的平分线 于点 ,连接 .求证:
(1) ;
(2)四边形 是平行四边形.
某农贸公司销售一批玉米种子,若一次购买不超过5千克,则种子价格为20元 千克,若一次购买超过5千克,则超过5千克部分的种子价格打8折.设一次购买量为 千克,付款金额为 元.
(1)求 关于 的函数解析式;
(2)某农户一次购买玉米种子30千克,需付款多少元?
为了解某地七年级学生身高情况,随机抽取部分学生,测得他们的身高(单位: ,并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题.
(1)填空:样本容量为 , ;
(2)把频数分布直方图补充完整;
(3)若从该地随机抽取1名学生,估计这名学生身高低于 的概率.

请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
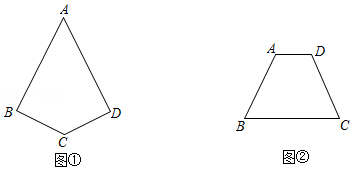
(1)如图①,四边形 中, , ,画出四边形 的对称轴 ;
(2)如图②,四边形 中, , ,画出 边的垂直平分线 .
(1)计算: ;
(2)解分式方程: .