如图1，四边形ABCD中，AD∥BC，∠A=90°，BD⊥CD，AD=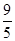
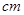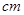，BC=5，动点P从点D出发，以1cm/s的速度沿DB方向运动，动点Q也从点D出发，以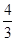
/
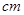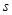的速度沿DC方向运动，P，Q两点同时出发，当点Q到达点C时停止运动，点P也随之停止，设运动时间为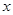
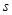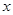（＞0）．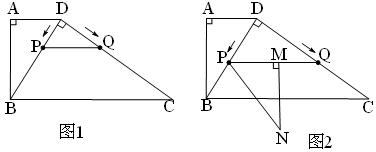
（1）求线段DB的长；
（2）请判断PQ与BC的位置关系，并加以证明；
（3）伴随P，Q两点的运动，将△DPQ绕点P旋转，得到△PMN，点M落在线段PQ上，若△PMN
与△DBC的重叠部分的图形周长为y，
①请求出y与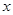之间的函数关系式，并指出自变量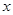的取值范围；
②求出当4＜y≤5时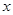的取值范围．
如图所示，在△ABC中，若AB=5，AC=2，
BAC=120°，以BC为边作等边三角形BCD，把△ABD绕D点按顺时针方向旋转60°到△ECD的位置。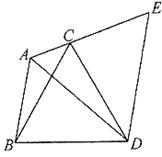
（1）求
BAD的度数；（2）求AE的长。
求抛物线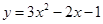
与两坐标轴的交点坐标及与坐标轴交点为顶点的三角形面积。
对于抛物线
.（1）它与x轴交点的坐标为，与y轴交点的坐标为，顶点坐标为；
（2）在坐标系中利用描点法画出此抛物线；
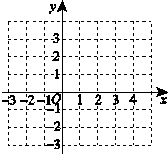
（3）利用以上信息解答下列问题：若关于x的一元二次方程
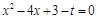（t为实数）在
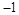＜x＜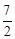
的范围内有解，则t的取值范围是．
随着人们节能意识的增强，节能产品的销售量逐年增加．某地区高效节能灯的年销售量2009年为10万只，预计2011年将达到14.4万只．求该地区2009年到2011年高效节能灯年销售量的平均增长率.
如图，正方形
中,点F在边BC上，E在边BA的延长线上.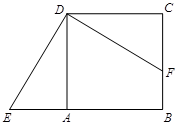
（1）若
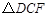按顺时针方向旋转后恰好与
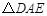重合.则旋转中心是点；最少旋转了度；（2）在（1）的条件下，若
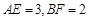，求四边形
的面积。