如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形,在建立平面直角坐标系后,点B的坐标为(﹣1,﹣1).
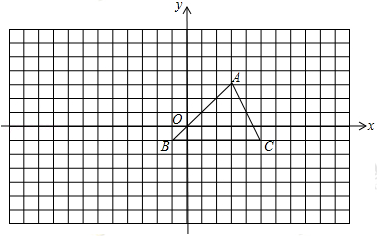
(1)把△ABC向右平移3格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;
(2)把△ABC绕点B按顺时针方向旋转90°后得到△A2B2C2,画出△A2B2C2的图形并写出点B2的坐标;
(3)直接写出C到AB的距离为 .
已知正比例函数y1=2x和一次函数y2=﹣x+b,一次函数的图象与x轴、y轴分别交于点A、点B,正比例函数的图象与一次函数的图象相交于点P.
(1)若P点坐标为(3,n),试求一次函数的表达式,并用图象法求y1≥y2的解;
(2)若S△AOP=3,试求这个一次函数的表达式;
(3)x轴上有一定点E(2,0),若△POB≌△EPA,求这个一次函数的表达式.
甲、乙两车分别从相距200千米的A、B两地同时出发相向而行,甲到B地后立即返回,乙到A地后停止行驶,下图是它们离各自出发地的距离y(km)与行驶时间x(h)之间的函数图象.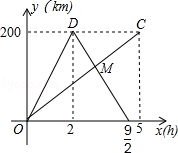
(1)请直接写出甲离出发地A的距离y(km)与行驶时间x(h)之间的函数关系式,并写出自变量x的取值范围;
(2)求出函数图象交点M的坐标并指出该点坐标的实际意义;
(3)求甲、乙两车从各自出发地驶出后经过多长时间相遇.
已知:如图,四边形ABCD中,AB>AD,AC平分∠DAB,∠B+∠D=180°.求证:CD=CB.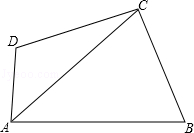
如图,边长为12cm的正方形纸片,点P为边BC的中点,折叠纸片使点A落在点P上,求AM的长.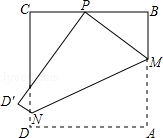
如图,在△MPN中,MP=NP,∠MPN=90°,S、P、Q在同一条直线上,NQ⊥PQ,MS⊥PS,垂足分别为Q、S,QS=8.4cm,NQ=2.1cm.试求出MS的长为多少cm.