把一副扑克牌中的三张黑桃牌（它们正面的数字分别为3,4,5）洗匀后正面朝下放在桌面上．小王和小李玩摸牌游戏，游戏规则如下：先由小王随机抽取一张牌，记下牌面数字后放回，洗匀后正面朝下，再由小李随机抽取一张牌，记下牌面数字．当两张牌的牌面数字相同时，小王赢；当两张牌的牌面数字不同时，小李赢．
（1）请利用画树状图或列表的方法表示出所有可能出现的结果；
（2）分析游戏规则对双方是否公平，并说明理由．
商场某种新商品每件进价是40元，在试销期间发现，当每件商品售价50元时，每天可销售500件，当每件商品售价高于50元时，每涨价1元，日销售量就减少10件．据此规律，请回答：
（1）当每件商品售价定为55元时，每天可销售多少件商品？商场获得的日盈利是多少？
（2）在上述条件不变，商品销售正常的情况下，每件商品的销售定价为多少元时，商场日盈利可达到8000元？
如图，AB是⊙O的直径，AM和BN是它的两条切线，DE切⊙O于点E，交AM于点D，交BN于点C，
（1）求证：OD∥BE；
（2）如果OD=6cm，OC=8cm，求CD的长；
（3）若F为CD的中点，连OF，试确定OF与CD的数量关系，并说明理由．
如图，在边长为2的圆内接正方形ABCD中，AC是对角线，P为边CD的中点，延长AP交圆于点E．
（1）∠E= 度；
（2）写出图中现有的一对不全等的相似三角形，并说明理由；
（3）求弦DE的长．
已知：▱ABCD的两边AB，AD的长是关于x的方程x2﹣mx+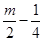
=0的两个实数根．
（1）当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；
（2）若AB的长为2，那么▱ABCD的周长是多少？
已知x=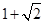
，求代数式
的值．