如图甲所示为学校操场上一质量不计的竖直滑竿，滑竿上端固定，下端悬空．为了研究学生沿竿的下滑情况，在竿顶部装有一拉力传感器，可显示竿顶端所受拉力的大小．现有一质量为50kg的学生（可视为质点）从上端由静止开始滑下，5s末滑到竿底时速度恰好为零．以学生开始下滑时刻为计时起点，传感器显示的拉力随时间变化情况如图乙所示，g取10m/s2．求：
（1）该学生下滑过程中的最大速度；
（2）滑竿的长度．
如图所示，重力为G的物体与水平地面间的动摩擦因数为
，现用绳子拉物体，绳子与水平面成30°角，若要使物体沿水平面匀速向右运动，则拉力F为多大？
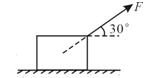
如图所示，水平桌面上有一轻弹簧，左端固定在A点，自然状态时其右端位于B点。水平桌面右侧有一竖直放置的光滑轨道MNP，其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧，MN为其竖直直径，P点到桌面的竖直距离也是R。用质量m1=0.4kg的物块将弹簧缓慢压缩到C点，释放后弹簧恢复原长时物块恰停止在B点。用同种材料、质量为m2=0.2kg的物块将弹簧缓慢压缩到C点释放，物块过B点后其位移与时间的关系为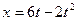
，物块飞离桌面后由P点沿切线落入圆轨道。g=10m/s2，求：
（1）物块过D点时的速度
（2）BD间的水平距离。
（3）判断m2能否沿圆轨道到达M点。
（4）释放后m2运动过程中克服摩擦力做的功
如图所示，长12m，质量100kg的小车静止在光滑水平地面上。一质量为50kg的人从小车左端，以4m/s2加速度向右匀加速跑至小车的右端（人的初速度为零）。求：
（1）小车的加速度大小；
（2）人从开始起跑至到达小车右端所经历的时间；
（3）人从开始起跑至到达小车右端对小车所做的功。
2007年10月24日，“嫦娥一号”卫星星箭分离，卫星进入绕地球轨道。在绕地运行时，要经过三次近地变轨：12小时椭圆轨道①→24小时椭圆轨道②→48小时椭圆轨道③→地月转移轨道④。11月5日11时，当卫星经过距月球表面高度为h的A点时，再一次实施变轨，
进入12小时椭圆轨道⑤，后又经过两次变轨，最后进入周期为T的月球极月圆轨道⑦。如图所示，已知月球半径为R。
（1）请回答：“嫦娥一号”在完成第三次近地变轨时需要加速还是减速？
（2）写出月球表面重力加速度的表达式。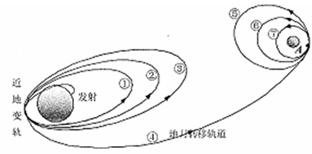
如右图所示，质量60kg的人站在水平地面上，通过定滑轮和绳（不计其摩擦和绳子质量）竖直向上提起质量为10kg的货物。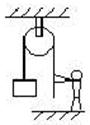
（1）货物以a1=2m／s2匀加速上升，人对地面压力多大？
（2）货物匀加速上升时，其最大加速度为多大（g取10m／s2）