已知数列{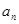 }满足
}满足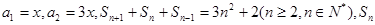 是数列{
是数列{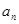 }的前n项和.
}的前n项和.
(1)若数列{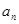 }为等差数列:
}为等差数列:
①求数列{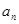 }的通项公式;
}的通项公式;
②若数列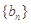 满足
满足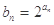 ,数列
,数列 满足
满足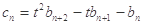 ,试比较数列
,试比较数列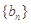 的前n项和
的前n项和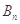 与
与 的前n项和
的前n项和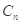 的大小;
的大小;
(2)若对任意的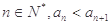 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.
如图,四棱锥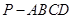 中,
中,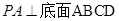 .
. ,F为PC的中点,
,F为PC的中点,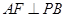 .
.
(1)求 的长:
的长:
(2)求二面角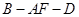 的正弦值.
的正弦值.
盒中共有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同
(1)从盒中一次随机抽出2个球,求取出的2个球颜色相同的概率:
(2)从盒中一次随机抽出4个球,其中红球,黄球,绿球的个数分别记为 ,随机变量X表示
,随机变量X表示 中的最大数,求X的概率分布列和数学期望
中的最大数,求X的概率分布列和数学期望 .
.
已知锐角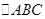 中,角A、B、C所对的边分别为a,b,c,且
中,角A、B、C所对的边分别为a,b,c,且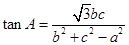
(1)求角A的大小:
(2)求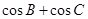 的取值范围.
的取值范围.
已知函数 .
.
(1)若对于 都有
都有 成立,试求a的取值范围;
成立,试求a的取值范围;
(2)记 ,当
,当 时,函数
时,函数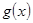 在区间
在区间 上有两个零点,求实数b的取值范围.
上有两个零点,求实数b的取值范围.
已知 ,其中
,其中 ,
,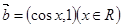 .
.
(1)求 的周期和单调递减区间;
的周期和单调递减区间;
(2)在△ABC中,角A,B,C的对边分别为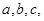
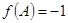 ,
, ,
, ,求边长
,求边长 和
和 的值(
的值( ).
).