设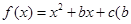 、
、 .
.
(Ⅰ)若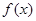 在
在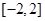 上单调,求
上单调,求 的取值范围;
的取值范围;
(Ⅱ)若 对一切
对一切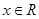 恒成立,求证:
恒成立,求证: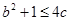 ;
;
(Ⅲ)若对一切满足 的实数
的实数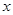 ,都有
,都有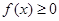 ,且
,且 的最大值为1,求证:
的最大值为1,求证: 、
、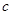 满足的条件是
满足的条件是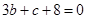 且
且
(本题满分12分) 盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得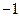 分 . 现从盒内任取3个球.
分 . 现从盒内任取3个球.
(Ⅰ)求取出的3个球颜色互不相同的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)(文科) 求取出的3个球中白色球的个数为2个的概率
(Ⅲ)(理科)设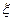 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求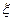 的分布列和数学期望.
的分布列和数学期望.
(本题满分12分)如图所示,四棱锥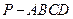 的底面为直角梯形,
的底面为直角梯形, ,
,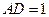 ,
,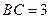 ,
,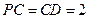 ,
,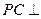 底面
底面 ,
,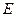 为
为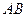 的中点.
的中点.
(Ⅰ)求证:平面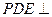 平面
平面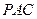 ;
;
(Ⅱ)求直线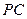 与平面
与平面 所成的角;
所成的角;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.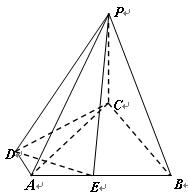
(本题满分12分) 已知函数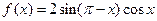 .
.
(Ⅰ)求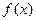 的最小正周期;
的最小正周期;
(Ⅱ)求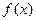 的对称轴方程;
的对称轴方程;
(Ⅲ)求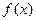 在区间
在区间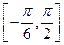 上的最大值和最小值.
上的最大值和最小值.
(本小题满分14分)
设数列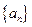 的前
的前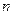 项和为
项和为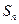 ,已知
,已知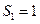 ,
,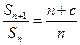 (
(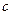 为常数,
为常数,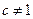 ,
,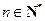 ),且
),且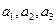 成等差数列.
成等差数列.
(1)求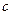 的值;
的值;
(2)求数列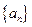 的通项公式;
的通项公式;
(3)若数列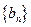 是首项为1,公比为
是首项为1,公比为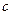 的等比数列,记
的等比数列,记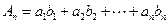 ,
, ,
,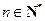 .证明:
.证明: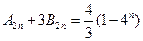 .
.
(本小题满分14分)
已知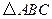 的周长为
的周长为 ,且
,且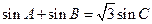 ,
,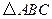 的面积为
的面积为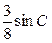 ,
,
(1)求边 的长;
的长;
(2)求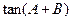 的值.
的值.