已知椭圆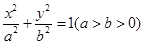 的右焦点为
的右焦点为 ,
,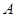 为短轴的一个端点,且
为短轴的一个端点,且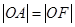 ,
,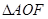 的面积为1(其中
的面积为1(其中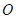 为坐标原点).
为坐标原点).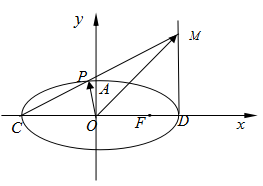
(1)求椭圆的方程;
(2)若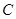 ,
,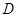 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点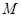 满足
满足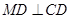 ,连接
,连接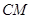 ,交椭圆于点
,交椭圆于点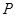 ,证明:
,证明: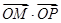 为定值.
为定值.
(本小题满分l2分)
若集合A={x|x2-2x-8<0},B={x|x-m<0}.
(1)若m=3,试求A∩(∁RB);
(2)若A∩B=∅,求实数m的取值范围;
(3)若A∩B=A,求实数m的取值范围.
(理数) 已知函数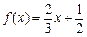 ,
,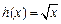 .
.
(Ⅰ)设函数F(x)=18f(x)-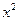 [h(x)]
[h(x)]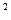 ,求F(x)的单调区间与极值;
,求F(x)的单调区间与极值;
(Ⅱ)设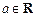 ,解关于x的方程
,解关于x的方程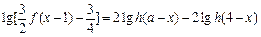 ;
;
(Ⅲ)设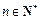 ,证明:
,证明: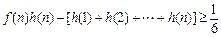 .
.
定义在R上的增函数y=f(x)对任意x,y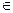 R都有f(x+y)=f(x)+f(y),则
R都有f(x+y)=f(x)+f(y),则
(1)求f(0)(2) 证明:f(x)为奇函数
(3)若 对任意
对任意 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围
(12分 ) .已知函数y=
) .已知函数y= f(x)=
f(x)= (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(1)试求函数f(x)的解析式
(2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说 明理由.
明理由.
(理数)某商场销售 某种商品的经验表明,该商品每日的销售量
某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格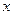 (单位:元/千克)满
(单位:元/千克)满 足关系式
足关系式 ,其中
,其中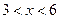 ,
,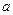 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克
(Ⅰ) 求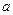 的值;
的值;
(Ⅱ) 若该商品的成品为3元/千克, 试确定销售价格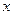 的值,使商场每日销售该
的值,使商场每日销售该 商品所获得的利润最大.
商品所获得的利润最大.