如图中电源的电动势E=12V,内电阻r=0.5Ω,将一盏额定电压为8V,额定功率为16W的灯泡与一只线圈电阻为0.5Ω的直流电动机并联后和电源相连,灯泡刚好正常发光,通电100min,问: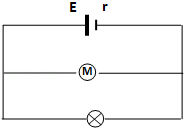
①电源提供的能量是多少?
②电流对电动机做功是多少?
③电动机的线圈产生的热量是多少?
④电动机的效率是多少?
我校一年一度的田径运动会已经举行。在4×100m接力赛的一组中有甲、乙两位同学,他们在奔跑时具有相同的最大速度。乙从静止开始全力奔跑,需跑出25m才能达到最大速度,这一过程可看做匀变速直线运动。现在甲持棒以最大速度向乙奔来,乙在接力区准备全力奔出。若要求乙接棒时奔跑速度达到最大速度的80%,回答下列问题:乙在接力区必须先跑出多少米?
乙应在距离甲多远时起跑?
一速度为v的高速α粒子(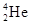 )与同方向运动的氖核(
)与同方向运动的氖核(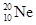 )发生弹性正碰,碰后α粒子恰好静止。求碰撞前后氖核的速度(不计相对论修正)。
)发生弹性正碰,碰后α粒子恰好静止。求碰撞前后氖核的速度(不计相对论修正)。
已知某金属表面接受波长为λ和2λ的单色光照射时,释放出光电子的最大初动能分别为30 eV和10 eV,求能使此种金属表面产生光电效应的入射光的极限波长为多少?(λ为未知量)
.氢原子光谱除了巴耳末系外,还有赖曼系、帕邢系等,其中帕邢系的公式为=
R(-)(n=4,5,6,…),R=1.10×107 m-1.若已知帕邢系的氢原子光谱在红外线区域,试求:
(1)n=6时,对应的波长;
(2)帕邢系形成的谱线在真空中的波速为多少?n=6时,传播频率为多大?
在氢原子中,如果电子从r1=0.53×10-10 m的轨道上,由于获得能量而进入r2=2.12×10-10 m的轨道上做匀速圆周运动,求在该轨道上电子的动能是多少?(k=9.0×109 N·m2/C2)