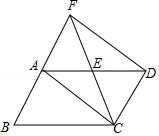
如图1：在四边形ABCD中，ABAD，∠BAD120°，∠B-优题课

如图1：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E，F分别是BC，CD上的点，且∠EAF=60°．探究图中线段BE，EF，FD之间的数量关系。
小王同学探究此问题的方法是，延长FD到点G，使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；
如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°．E，F分别是BC，CD上的点，且∠EAF=∠BAD，上述结论是否仍然成立，并说明理由。

科目数学题型解答题难度中等

知识点：三角形的五心

如图， $Rt Δ ABC$ 中， $∠ ABC = 90 °$ ，以点 $C$ 为圆心， $CB$ 为半径作 $⊙ C$ ， $D$ 为 $⊙ C$ 上一点，连接 $AD$ 、 $CD$ ， $AB = AD$ ， $AC$ 平分 $∠ BAD$ ．

（1）求证： $AD$ 是 $⊙ C$ 的切线；

（2）延长 $AD$ 、 $BC$ 相交于点 $E$ ，若 $S_{ΔEDC} = 2 S_{ΔABC}$ ，求 $\tan ∠ BAC$ 的值．

为了做好防疫工作，学校准备购进一批消毒液．已知2瓶 $A$ 型消毒液和3瓶 $B$ 型消毒液共需41元，5瓶 $A$ 型消毒液和2瓶 $B$ 型消毒液共需53元．

（1）这两种消毒液的单价各是多少元？

（2）学校准备购进这两种消毒液共90瓶，且 $B$ 型消毒液的数量不少于 $A$ 型消毒液数量的 $\frac{1}{3}$ ，请设计出最省钱的购买方案，并求出最少费用．

如图，点 $C$ 是 $BE$ 的中点，四边形 $ABCD$ 是平行四边形．

（1）求证：四边形 $ACED$ 是平行四边形；

（2）如果 $AB = AE$ ，求证：四边形 $ACED$ 是矩形．

为了参加全市中学生“党史知识竞赛”，某校准备从甲、乙2名女生和丙、丁2名男生中任选2人代表学校参加比赛．

（1）如果已经确定女生甲参加，再从其余的候选人中随机选取1人，则女生乙被选中的概率是　　；

（2）求所选代表恰好为1名女生和1名男生的概率．

端午节吃粽子是中华民族的传统习俗．某食品厂为了解市民对去年销量较好的 $A$ 、 $B$ 、 $C$ 、 $D$ 四种粽子的喜爱情况，在端午节前对某小区居民进行抽样调查（每人只选一种粽子），并将调查情况绘制成两幅尚不完整的统计图．

根据以上信息，解答下列问题：

（1）补全条形统计图；

（2）扇形统计图中， $D$ 种粽子所在扇形的圆心角是　　 $°$ ；

（3）这个小区有2500人，请你估计爱吃 $B$ 种粽子的人数为　　．

试卷网试题网古诗词网作文网范文网