如图,平面上有四个点A、B、C、D,根据下列语句画图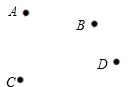
(1)画直线AB; 作射线BC;画线段CD;
(2)连接AD,并将其反向延长至E,使DE=2AD;
(3)找到一点F,使点F到A、B、C、D四点距离和最短.
两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且使PM=PN.
如图,抛物线 (
( )与
)与 轴相交于
轴相交于 两点,点
两点,点 是抛物线的顶点,以
是抛物线的顶点,以 为直径作圆
为直径作圆 交
交 轴于
轴于 两点,
两点, .
.
(1). 用含 的代数式表示圆
的代数式表示圆 的半径
的半径 的长;
的长;
)
(2). 连结 ,求线段
,求线段 的长;
的长;
(3). 点 是抛物线对称轴正半轴上的一点,且满足以
是抛物线对称轴正半轴上的一点,且满足以 点为圆心的圆
点为圆心的圆 与直线
与直线 和圆
和圆 都相切,求点
都相切,求点 的坐标.
的坐标.
)
某私营玩具厂招工广告称:“本厂工人工作时间:每天工作8小时,每月工作25天;待遇:熟练工人按计件付工资,多劳多得,且计件工资不少于1000元时,每月另加福利工资100元,按月结算……”.该厂只生产两种玩具:小狗和小汽车,熟练工人晓凤一月份领工资1145元,她记录了如下一些数据:
(1). 根据表格中的信息,试求出做1个小汽车所需时间和计件工资各是多少?
(2). 设晓凤某月生产小狗x个,小汽车y个,月工资(计件工资+福利工资=月工资)为W元.试求W与x的函数关系式.(不需写出自变量x的取值范围)
8分
(3). 有一天,厂方从销量方面考虑,对生产作了调整:每个工人每月生产小狗的个数不少于生产小汽车个数的2倍,假设晓凤的工作效率不变,且服从厂家安排,请运用数学知识说明厂家招工广告是否有欺诈行为.
0分

汽车在行驶中,由于惯性作用,刹车后,还要向前滑行一段距离才能停住,我们称这段距离为“刹车距离”,刹车距离是分析事故的一个重要因素.在一个限速 千米/小时以内的弯道上,甲、乙两车相向而行,发现情况不对后同时刹车,但还是相碰了.事后现场测得甲车的刹车距离为
千米/小时以内的弯道上,甲、乙两车相向而行,发现情况不对后同时刹车,但还是相碰了.事后现场测得甲车的刹车距离为 米,乙车的刹车距离超过
米,乙车的刹车距离超过 米,但小于
米,但小于 米.查有关资料知,甲车的刹车距离
米.查有关资料知,甲车的刹车距离 (米)与车速
(米)与车速 (千米/小时)的关系为
(千米/小时)的关系为
 ;乙车的刹车距离
;乙车的刹车距离 (米)与车速
(米)与车速 (千米/小时)的关系如右图所示.请你就两车的速度方面分析这起事故是谁的责任.
(千米/小时)的关系如右图所示.请你就两车的速度方面分析这起事故是谁的责任.
已知 ,延长BC到D,使
,延长BC到D,使 .取
.取 的中点
的中点 ,连结
,连结 交
交 于点
于点 .
.
(1). 求 的值;(2). 若
的值;(2). 若 ,求
,求 的长.
的长.